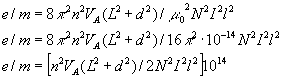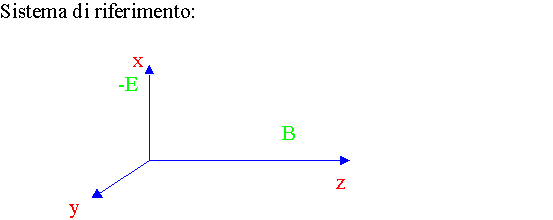
Misura di e/m con il metodo di Hoag
Velocita’ dell’elettrone alla fine dello stadio d’accelerazione:
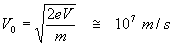
tempo trascorso tra le placchette deflettrici:
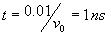
spostamento laterale:
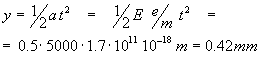
velocita’ perpendicolare:
cioe’ l’elettrone, se si ignora B, si sposta lateralmente di soli 0.42 mm, mentre acquista una velocita’ trasversa di 8.5 105 m/s.
Trattazione semplificata:
Ignoriamo l’effetto di B nell’intervallo di tempo (1 ns) che l’elettrone trascorre tra le armature.
Vt= velocita’ nel piano trasverso all’uscita delle armature.
w
= (e/m) Br = (m/e) Vt /B
Velocita’ angolare indipendente dal raggio del cerchio
Elettroni su orbite di raggio maggiore viaggiano piu’ velocemente.
Dato il potenziale acceleratore V, la velocita’ iniziale sara’:
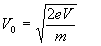
tempo per raggiungere lo schermo:
se tale tempo uguaglia quello che occorre per un giro completo:
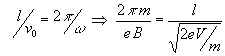
segue:
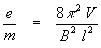
Focalizzazioni successive (rotazioni di multipli di 2
p) danno:
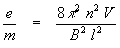
Relazioni "esatte":
Poniamo:
; 
; 
; 
;
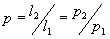
Equazioni che tengono conto del moto dell’elettrone tra le armature (tenendo conto sia di B che di E):
Verifichiamo sotto quali condizioni l’equazione esatta da’ il medesimo risultato di quella originale.
Poniamo:
L’equazione originale:
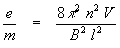
si puo’ modificare come segue:
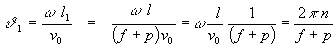
poniamo f=0.5 e diamo a p un valore arbitrario (e.g. 5):
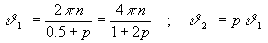
Sostituendo nelle espressioni di x ed y, si trova:
X = 0
Y = 0.06 a/
w2 = 1.8 mm
Avendo preso: E = 5000 V/m, d (distanza tra le armature) 1 cm e
B = 4 10-3 T
Quindi l’approssimazione e’ buona.
MISURA DI e/m CON IL METODO DI HOAG
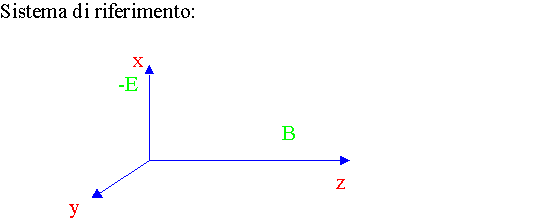
Calcolo dettagliato delle coordinate del punto d'arrivo sullo schermo:
Per lo studio del moto dividiamo i calcoli in due parti:
La prima parte integra le equazioni del moto all'interno delle piastre deflettrici, la seconda si occupa del moto dall'uscita delle piastre allo schermo del tubo catodico.
Sia v
o la velocita' che l'elettrone acquista grazie alla d.d.p. VA tra il catodo e l'anodo del tubo catodico, cioe` la velocita' dell’elettrone prima di entrare tra le armature deflettrici:
In presenza del solo campo elettrico avrei:
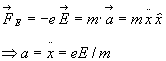
Questa accelerazione genera una componente della velocita' lungo l'asse x che chiamo v
n, e quindi la carica risente di una forza dovuta al campo magnetico, che e' diretto come l'asse z.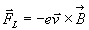 
Sull'elettrone avro' percio' una risultante:
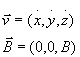
Calcoliamo il prodotto vettoriale:
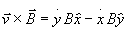
Risolviamo il moto componente per componente:
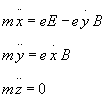
Ponendo:
avro':
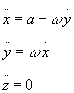
Introducendo ora la variabile complessa:
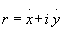
sommando le prime due equazioni del sistema abbiamo:
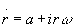
La soluzione di questa equazione differenziale e':
con c costante appartenente ai numeri complessi da determinarsi in base alla condizioni iniziali.
Ponendo:
e ricordando la definizione di r, possiamo scrivere:
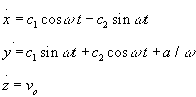
Poiche' a t=0 come condizioni al contorno abbiamo
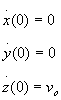
ricaviamo
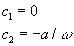
Riscrivo le equazioni:
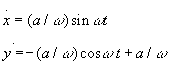
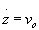
Se integriamo ulteriormente ricaviamo le equazioni del moto.
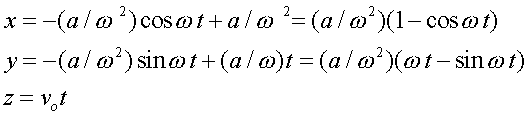
Il moto e' una cicloide. All'uscita delle piastre, dopo un tempo t
1=l1/vo, indicando con : 
le coordinate dell'elettrone saranno:
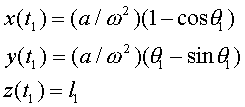
e le velocita' :
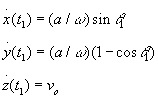
Nella seconda parte del moto abbiamo E = 0 , cioe' a = 0.
Le equazioni del moto risultano essere:
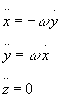
Integrando tali equazioni con il metodo gia’ impiegato, otteniamo:
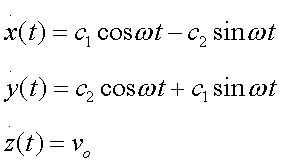
Imponendo come condizione iniziale la velocita' con cui l'elettrone e' uscito dalle piastre ricaviamo:
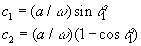
Integrando nuovamente le equazioni che esprimono le velocita' e imponendo come condizione iniziale la posizione dell'elettrone all'uscita delle piastre, otteniamo le equazioni del moto:
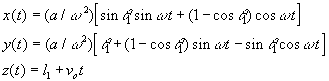
L'elettrone allora giunge sullo schermo al tempo:
misurato a partire dall’istante in cui esso e’ uscito dalle piastre.
Indichiamo con :
Percio' le coordinate dell'elettrone sullo schermo sono:
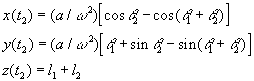
Questa è la formula che useremo per il calcolo di e/m.
Le grandezze che compaiono sono:
n = numero di giri compiuti dall’elettrone
L = lunghezza del solenoide
d = diametro del solenoide
V
A = potenziale acceleratore
N = numero di spire del solenoide
l = lunghezza efficace percorsa dagli elettroni lungo l'asse z
I = corrente che circola nel solenoide
Dimostriamo come si giunge all’equazione.
Ricordiamo alcune equazioni introdotte precedentemente:
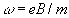
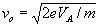
Il numero di giri che l’elettrone compie in un tempo t = l/v
o è:
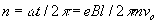
Sullo schermo si visualizza un punto quando ogni elettrone compie un numero intero n di giri. Se B(n) è il valore del campo magnetico per cui avviene tale contrazione, imponendo
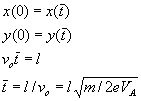
otteniamo:
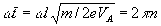
Elevando al quadrato e sostituendo il valore della velocità angolare ricaviamo:
In un solenoide infinito il campo magnetico vale:
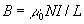
Nel nostro caso, avendo lunghezza finita, il campo sull’asse del solenoide vale:
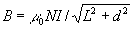
Sostituendo questo valore di B e ricordando che
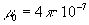
abbiamo:
