Onde meccaniche ed acustiche

Alcune relazioni di uso frequente

 

 

Vibrazione monocromatica:

 

 

In forma complessa:

 

 

U = ampiezza complessa

f= fase al tempo t=0

w= 2pn=pulsazione; con n= frequenza

 

Ampiezza relativa alla somma di due vibrazioni:

 

 

In notazione reale:

 

 

Vibrazioni quasi monocromatiche:

 

  1. in forma reale:

    2.  

     

    con A(t) funzione lentamente variabile di t

     

  2. in forma complessa:

 

 

 

 

 

Esempi di vibrazioni quasi monocromatiche:

 

  1. sinusoide smorzata esponenzialmente:

    2.  

     

     

    dove t >> 2p/w0

     

     

  2. sinusoide troncata

 

 

 

dove t >> 2p/w0

 

Rappresentazione spettrale della vibrazione (trasformata di Fourier)

 

 

  1. caso della sinusoide smorzata:

    2.  

     

  2. caso della sinusoide troncata:

 

 

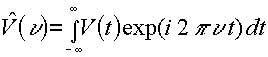
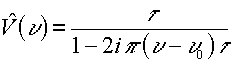
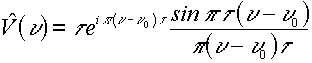
Energia associata a ciascuna componente spettrale:

 

 

  1. caso della sinusoide smorzata:

    2.  

     

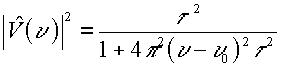
    (Lorenziana con larghezza totale a meta' altezza: 1/pt)

     

  2. caso della sinusoide troncata:

 

 

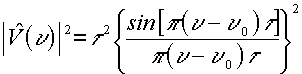
(Larghezza a meta' altezza Dn1/2 ~ 0.89/t)

 

 

 

Addizione di N vibrazioni monocromatiche (tipo Fabry-Perot):

 

 

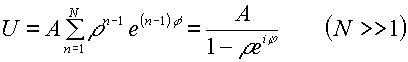
con:

 

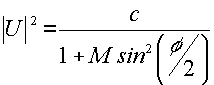
dove:

 

 

 

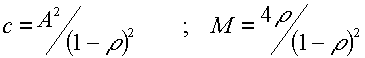
Addizione di N vibrazioni monocromatiche (tipo Fraunhofer):

 

 

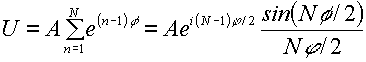
con:

 

 

 

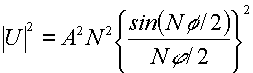
che definisce la funzione reticolo R(f) moltiplicata per A2N2

 

 

La funzione reticolo e' pari. Tra due massimi principali successivi esistono (N-2) massimi secondari.

 

 

Equazione delle onde in una dimensione (x):

 

 

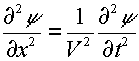
y=y(x,t)

 

Nel caso di una corda tesa:

 

 

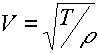
T = tensione cui la fune e' assoggettata

r = densita' lineare di massa

 

Nel caso di un tubo pieno di gas:

 

 

 

 

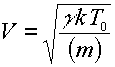
Con:

 

g= Cp/Cv ;

k = costante di Boltzmann;

T0 = Temperatura assoluta;

(m) = peso molecolare

 

Forma generale della soluzione dell'equazione delle onde in una dimensione:

 

 

Somma di un onda progressiva e di una regressiva, con ugual modulo della velocita'.

 

Equazione delle onde nello spazio:

 

 

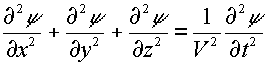
o anche:

 

 

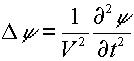
Soluzione generale nel caso di un'onda piana:

 

 

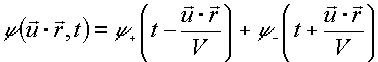
con:

 

 

Equazione delle onde nel caso di un'onda sferica:

 

 

 

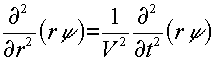
Soluzione generale:

 

 

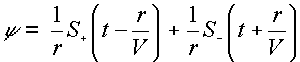
Onda piana monocromatica:

 

 

 

 

 

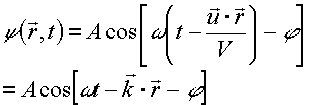
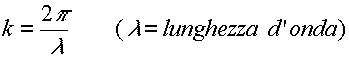
In notazione complessa:

 

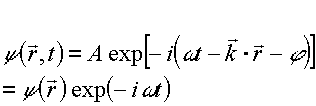
Onda monocromatica quasi piana:

 

 

Con A funzione di r che varia lentamente rispetto a F(r)

 

Y(r) soddisfa l'equazione di Helmotz: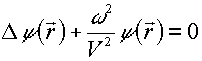

 

Velocita' di fase per l'onda quasi piana:

 

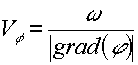
Energia media trasportata da un'onda:

 

 

Onde stazionarie:

 

 

Caso unidimensionale:

 

 

In tal caso sia la f che la g soddisfano l'equazione delle onde.

Soluzione:

 

 

Onda unidimensionale con la condizione al contorno y(0,0)=0:

 

 

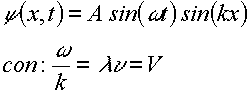
Onda unidimensionale con le condizioni al contorno

y(0,0)= y(L,0)=0 (e.g. fune fissa alle due estremita'):

 

 

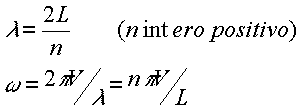
Battimenti tra due onde sinusoidali di frequenze vicine w1 ed w2

 

 

 

 

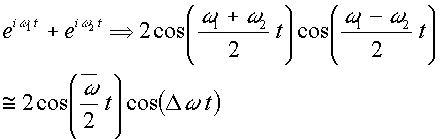
Effetto Doppler longitudinale:

 

 

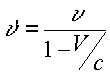
(sorgente che si muove con velocita' V verso l'osservatore;

c e' la velocita' dell'onda nel mezzo)