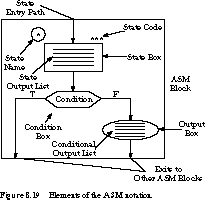
(ASM) notation and hardware description
languages (HDLs). ASMs are similar to program
flowcharts, but they have a more rigorous concept of timing. HDLs look much
like modern programming languages, but they explicitly support computations
that can occur in parallel. 
Each major unit, called an ASM block, consists of a state box and, optionally,
a network of condition and output boxes. A state machine is in exactly one
state or ASM block during the stable portion of the state time.
State Boxes There is one state
box per ASM block, reached from other ASM blocks through a single state
entry path. In addition, for each combination of inputs there is a single
unambiguous exit path from the ASM block. The state box is identified by
a symbolic state name-in a circle-and a binary-encoded state code, and it
contains an output signal list.
The output list describes the signals that are asserted
whenever the state is entered. Because signals may be expressed in either
positive or negative logic, it is customary to place an "L." or
"H." prefix before the signal name, indicating whether it is asserted
low or high. You can also specify whether the signal is asserted immediately
(I) or is delayed (no special prefix)
until the next clocking event. A signal not mentioned in the output list
is left unasserted.
Condition Boxes The condition box
tests an input to determine an exit path from the current ASM block to the
block to be entered next. The order in which condition boxes are cascaded
has no effect on the determination of the next ASM block.
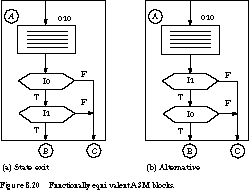
Figure 8.20(a) and (b)
show functionally equivalent ASM blocks: state B is to be entered
next if I0 and I1 are both 1; otherwise state C
is next.
Output Boxes Any output boxes on
the path from the state box to an exit contain signals that should be asserted
along with the signals mentioned in the state box. The state machine advances
from one state to the next in discrete rather than continuous steps. In
this sense, ASM charts have different timing semantics than program flowcharts.
Example The Parity Checker As an
example, we give the parity checker's ASM chart in Figure 8.21.
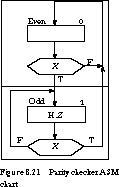
It consists of two states, Even and Odd, encoded as 0 and 1, respectively.
The input is the single bit X; the output is the single bit Z,
asserted high when the finite state machine is in the Odd state.
We can derive the state transition table from the ASM
chart. We simply list all the possible transition paths from one state to
another and the input combinations that cause the transition to take place.
For example, in state Even, when the input is 1, we go to state Odd. Otherwise
we stay in state Even. For state Odd, if the input is 1, we advance to Even.
Otherwise we remain in state Odd. The output Z is asserted only
in state Odd. The transition table becomes:
| Input X | Present State | | Next State | Output Z |
|---|---|---|---|---|
| F | Even | | Even | Not asserted |
| T | Even | | Odd | Not asserted |
| F | Odd | | Odd | Asserted |
| T | Odd | | Even | Asserted |
Example Vending Machine Controller We
show the ASM chart for the vending machine in Figure 8.22.
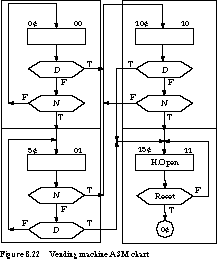
To extract the state transition table, we simply examine all exit paths
from each state. For example, in the state 0˘, we advance to state
10˘ when input D is asserted. If N is asserted, we
go to state 5˘. Otherwise, we stay in state 0˘. The rest of the
table can be determined by looking at the remaining states in turn.
(VHSIC hardware description language)
is an industry standard. Although its basic concepts are relatively straightforward,
its detailed syntax is beyond the scope of this text. However, we can illustrate
its capabilities for describing finite state machines by examining a description
of the parity checker written in VHDL: ENTITY parity_checker IS PORT ( x, clk: IN BIT; z: OUT BIT); END parity_checker;
ARCHITECTURE behavioral OF parity_checker IS BEGIN main: BLOCK (clk = `1' and not clk'STABLE)
TYPE state IS (Even, Odd); SIGNAL state_register: state := Even;
BEGIN state_even: BLOCK ((state_register = Even) AND GUARD) BEGIN state_register <= Odd WHEN x = `1' ELSE Even END BLOCK state_even;
BEGIN state_odd: BLOCK ((state_register = Odd) AND GUARD) BEGIN state_register <= Even WHEN x = `1' ELSE Odd; END BLOCK state_odd;
z <= `0' WHEN state_register = Even ELSE `1' WHEN state_register = Odd; END BLOCK main; END behavioral;Every VHDL description has two components: an interface description and an architectural body. The former defines the input and output connections or "ports" to the hardware entity being designed; the latter describes the entity's behavior.
is a guard that evaluates to true whenever the clock signal has recently undergone a 0-to-1 transition. The main block is enabled for evaluation when this particular guard becomes true.clk = `1' and not clk'stable
module parity title 'odd parity checker state machine Joe Engineer, Itty Bity Machines, Inc.' u1 device 'p22v10';
"Input Pins clk, X, RESET pin 1, 2, 3;
"Output Pins Q, Z pin 21, 22; Q, Z istype 'pos,reg';
"State registers SREG = [Q, Z]; EVEN = [0, 0]; " even number of 0's ODD = [1, 1]; " odd number of 0's
equations [Q.ar, Z.ar] = RESET; "Reset to state S0
state_diagram SREG state EVEN: if X then ODD else EVEN; state ODD: if X then EVEN else ODD;
test_vectors ([clk, RESET, X] -> [SREG]) [0,1,.X.] -> [EVEN]; [.C.,0,1] -> [ODD]; [.C.,0,1] -> [EVEN]; [.C.,0,1] -> [ODD]; [.C.,0,0] -> [ODD]; [.C.,0,1] -> [EVEN]; [.C.,0,1] -> [ODD]; [.C.,0,0] -> [ODD]; [.C.,0,0] -> [ODD]; [.C.,0,0] -> [ODD]; end parity;An ABEL description consists of several sections: module, title, descriptions, equations, truth tables, state diagrams, and test vectors, some of which are optional. Every ABEL description begins with a
module statement and an
optional title statement. These name the module and provide
some basic documentation about its function.description section.
The elements of this section are the kind of device being programmed, the
specification of inputs and outputs, and the declaration of which signals
constitute the state of the finite state machine.(REG) associated
with particular output pins. The P22V10 PAL also supports negative logic
outputs as well as outputs that bypass the internal flip-flops.equation section defines outputs in
terms of Boolean equations of the inputs. In this case, the asynchronous
reset (.ar) inputs of the Q and Z flip-flops
are driven high when the RESET signal is asserted.state_diagram section describes the
transitions among states using a programming language-like syntax. If we
are in EVEN and the input X is asserted, we change to ODD. Otherwise
we stay in EVEN. Similarly, if we are in ODD and X is asserted,
we return to EVEN. Other-wise we stay in state ODD. ABEL supports a variety
of control constructs, including such things as case statements.test_vectors.
This is a tabular listing of the expected input/output behavior of the finite
state machine. The first entry describes what happens when RESET is asserted:
independent of the current value of X, the machine is forced to
EVEN. The rest of the entries describe the state sequence for the input
string 111011000. The ABEL system simulates the description to ensure that
the behavior matches the specified behavior of the test vectors.