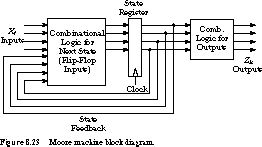
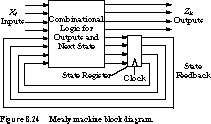
See Figure 8.24. The outputs can change immediately after a change at the inputs, independent of the clock. A Mealy machine constructed in this fashion has asynchronous -outputs.


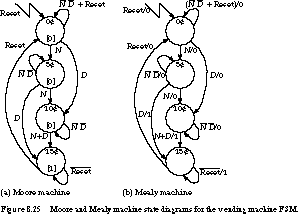
Figure 8.25 shows the notations for Mealy and Moore state diagrams, using the vending machine example. For Moore machines, the outputs are associated with the state in which they are asserted. Arcs are labeled with the input conditions that cause the transition from the state at the tail of the arc to the state at its head. Combinational logic functions are perfectly acceptable as arc labels.
In Mealy machines, the outputs are associated with
the transition arcs rather than the state bubble. A slash separates the
inputs from the outputs. For example, if we are in state 10Ę and either
N or D is asserted, Open will be asserted. Any glitch
on N or D could cause the gum to be delivered by mistake.
The state diagrams in this figure are labeled more completely
than our previous examples. For example, we make explicit the transitions
that cause the machine to stay in the same state. We usually eliminate such
transitions to simplify the state diagram. We also associate explicit output
values with each transition in the Mealy state diagram and each state in
the Moore state diagram. A common simplification places the output on the
transition or in the state only when it is asserted. You should clarify
your assumptions whenever you draw state diagrams.
Consider a finite state machine that asserts its single output whenever its input string has at least two 1's in sequence. The minimum Moore and Mealy state diagrams are shown in Figure 8.26.
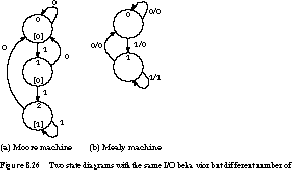
The equivalent ASM charts are in Figure 8.27.
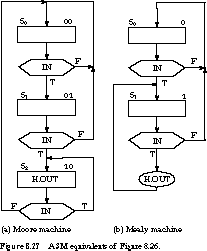
To represent the 1's sequence, the Moore machine requires two states
to distinguish between the first and subsequent 1's. The first state has
output 0, while the second has output 1. The Mealy machine accomplishes
this with a single state reached by two different transitions. For the first
1, the transition has output 0. For the second and subsequent 1's, the transition
has output 1. Despite the Mealy machine's timing complexities, designers
like its reduced state count.
Example Moore Machine Description†To
better understand the timing behavior of Moore and Mealy machines, let's
begin by reverse engineering some finite state machines. We will
work backward from a circuit-level implementation of the finite state machine
to derive an ASM chart or state diagram that describes the machine's behavior.
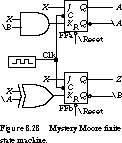
Figure 8.28 shows schematically a finite state machine with single data
input X and output Z. The FSM is a Moore machine because
the output is a combinational logic function (in this case
a trivial one) of the state alone. The state register is implemented
by two master/slave J-K flip-flops, named A and
B, respectively. The machine can be in any one of up to four valid
states. The output Z and the state bit B are the same.
Signal Trace Method†There are two
systematic approaches to determining the state transitions: exhaustive
signal tracing and extraction of the next state/output functions.
We examine the former here and the latter in the next subsection.
Signal tracing uses a collection of input sequences to
exercise the various state transitions of the machine. To see how it works,
let's start by generating a sample input sequence.
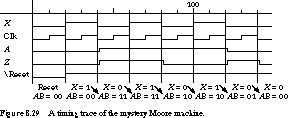
It is reasonable to assume that the FSM is initially reset and that it
has been placed in state A = 0, B =
0. Figure 8.29 contains the timing waveform you would see after presenting
the input sequence 1 0 1 0 1 0 to the machine. Because the FSM is implemented
with master/slave flip-flops, the state time begins with the falling edge
of the clock. Input X must be stable throughout the high time of
the clock to guard against ones catching problems.
The sequence of events in Figure 8.29 is as follows. The
asserted reset signal places the FSM in state 00. After the falling edge,
input X goes high just after time step 20. At the next rising edge,
the input is sampled and the next state is determined, but this is not presented
to the outputs until the falling edge at time step 40. After a short propagation
delay, the state becomes 11. We express the transition as "a 1 input
in state 00 leads to state 11."
During the next state time, X is 0, and the FSM
stays in state 11 as seen at time step 60. X now changes to 1,
and at the next falling edge the state changes to 10.
The input next changes to 0, causing the state machine
to remain in state 10 at time step 100. A transition to 1 causes it to change
to state 01 after time step 120. The final transition to 0 leaves the machine
in state 00.

Figure 8.30 contains the partial transition table we deduce from this
input sequence. We would have to generate additional input sequences to
fill in the missing transitions. For example, an input sequence from the
reset state starting with a 0 would fill in the missing transition from
state 00. The sequence 1 1 1 1, tracing from state 00 to 11 to 10 to 01,
would catch the remaining transition.
Next State/Output Function Analysis†Signal
tracing is acceptable for a small FSM, but it becomes intractable for more
complex finite state machines. With a single input and 2 bits of state,
the example FSM has eight different transitions, two from each of four states.
And the number of combinations doubles for each additional input bit and
doubles again for each state bit.
Our alternative method derives the next-state functions
directly from the combinational logic equations at the flip-flop inputs
and the output function from the flip-flop outputs. For the mystery machine,
these are
We can now express the flip-flop outputs, AJa =X†† Ka=X††Z
=B Jb=X Kb=X›
+
and B+, in terms of the excitation equations for the
J-K flip-flop. We simply substitute the logic functions
at the inputs into the excitation equations:
A +=Ja
+A
=X
+(
+B)A B+=Jb
+B
=X
+(X
+A
)B
+
and B+, are now expressed in terms of the current
state, A and B, and the input X. We show the
K-maps that correspond to these functions in Figure 8.31. 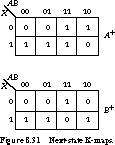
The missing state transitions are now obvious. In state
00 with input 0, the next state is A+ =
0 and B+ = 0. In state 01 with input
1, the next state is A+ = 1, B+
= 1. With its behavior no longer a mystery, we show the ASM
chart for this finite state machine in Figure 8.32.
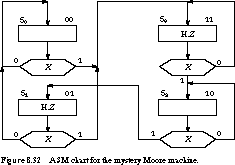
In the figure, we assume the following symbolic state assignment: S0
= 00, S1 = 01, S2 =
10, S3 = 11.
Example Mealy Machine Description†Continuing
with our reverse engineering exercise, consider the circuit of Figure 8.33.
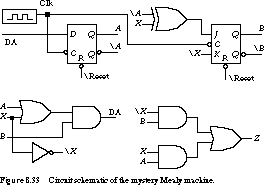
Once again, the FSM has one input, X, and one output, Z. This time the output is a function of the current state, denoted by A and B, and the input X. The state register is implemented by one D flip-flop and one master/slave J-K flip-flop.
Before examining a signal trace, we must understand
the conditions under which the Mealy machine's inputs are sampled and the
outputs are valid. The next state is computed from the current state and
the inputs, so exactly when are the inputs sampled? The answer depends on
the kinds of flip-flops used to implement the state register. In the example,
our use of a master/slave flip-flop dictates that the inputs must be stable
during the high time of the clock (to avoid ones catching)
and must be valid a setup time before the falling edge.
Technically, the outputs are valid only at the end
of the state time, determined by the falling edge of the clock. In other
words, the output for the current state is valid just as the machine enters
its next state! If we are using a master/slave flip-flop and if the inputs
do not change during the high time of the clock, then the outputs may also
be valid during the clock high time.
Negative edge-triggered systems require that the inputs
be stable before the falling edge that delineates the state times. This
means that the outputs cannot be determined until just before the falling
edge. The output remains valid only as long as it takes to compute a new
output in the new state.
Similarly, for positive edge-triggered systems the outputs
are valid at the rising edge. Again, the output is considered valid just
before the clock edge that causes the machine to enter its new state.
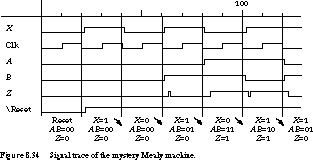
Figure 8.34 gives the timing waveform that corresponds to the input sequence
10101, after a reset to state 00. In state 00, reading a 1 keeps the machine
in state 00 (time step 40).
Reading a 0 then advances the machine to state 01 (time
step 60). The waveform for output Z has a glitch.
The valid output is determined only at the end of the state time. In this
case, the output is 0.
A 1 in state 01 leads to state 11 (time
step 80). Again, the output in this state is the value of Z
at the falling edge and thus is 1.
Reading a 0 in state 11 moves us to state 10 (time
step 100), with the output continuing to be asserted despite
the momentary glitch.
A 1 in state 10 leads us to state 01 (time
step 120). The output goes low and will stay that way as long
as the input X stays high.
We show the partial state transition table in Figure 8.35.

The input sequence produced only five of the eight state transitions.
To complete the state diagram, we would have to generate additional sequences
to traverse the missing transitions.
Alternatively, we can discover the complete set of transitions
by analyzing the next-state and output functions directly, just as we did
in the Moore machine:
Since A is a D flip-flop, the function for AA +=B(A+X)=A B+B X B+=Jb
+B
=(› X
)
+B
=(
+A X)
+X B=AX
+


+B X Z=A X+B
+ is exactly the combinational logic function
at its input. B is a J-K flip-flop, so we determine
the function for B+ by substituting the logic functions
at the J and K inputs into the J-K excitation
function.
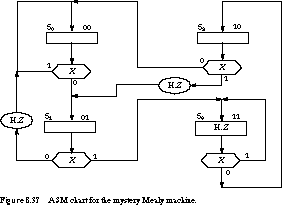
We give the next-state and output K-maps in Figure 8.36.
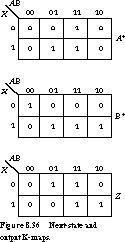
The missing transitions are from state 01 to 00 on input 0, 10 to 00
on input 0, and 11 to 11 on input 1. The respective outputs are 1, 0, and
1. Assuming that S0, S1, S2, and S3
correspond to encoded states 00, 01, 10, 11, we show the ASM chart for the
mystery machine in Figure 8.37.
States, Transitions, and Outputs in Mealy and
Moore Machines†Suppose that a given state machine has M
inputs and N outputs and is being implemented using L
flip-flops. You might ask a number of questions to bound the complexity
of this state machine. For example, what are the minimum and maximum numbers
of states that such a machine might have? With L flip-flops, the
implementation has the power to represent 2L states. But for a specific
FSM as few as 1 and as many as 2L of these might be valid states.
What are the minimum and maximum numbers of state transitions
that can begin in a given state? Since there must be an exit transition
for each possible input combination, the minimum and the maximum are the
same: 2M transitions.
A similar question involves the minimum and maximum numbers
of state transitions that can end in a given state. Because we can have
start-up states reachable only on reset, the minimum number of input transitions
is 0. Since a single state could conceivably be the target of all the transitions
of the finite state machine, the maximum number of input transitions is
2M * 2L, the number of possible input combinations multiplied by the number
of states.
A final question is the minimum and maximum numbers of patterns that
can be observed on the machine's outputs. The minimum number of unique output
patterns is 1, of course. Every state and every transition can be associated
with the same pattern.
The maximum number depends on the kind of machine. For
a Mealy machine, the maximum number of output patterns is the smaller of
the number of transitions, 2M * 2L, or the number of possible output patterns,
2N. If the number of transitions exceeds the number of possible output patterns,
then some must be repeated. In the Moore machine, the maximum is the smaller
of the number of states, 2L, and the number of possible output patterns,
2N. If the number of states exceeds the number of output patterns, then
some patterns will also need to be repeated.
As an example, consider a Moore machine with two inputs,
one flip-flop, and three outputs. The state, transition, and output bounds
are:
(per state):
4
(per state):
4
(per state):
0
(per state):
8
One way to do this is to synchronize the Mealy machine outputs with output flip-flops. See Figure 8.38.
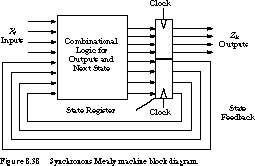
The flip-flops are clocked with the same edge as the state register.
This has the effect of converting the Mealy machine into a Moore machine,
by making the outputs part of the state encoding! However, this machine
does not have exactly the same input/output behavior as the original Mealy
machine (can you figure out why?). We will have
more to say about synchronous Mealy machines in Chapter 10.
Discussion†In general, fully
synchronous finite state machines are much easier to implement and debug
than asynchronous machines. If you were using discrete TTL components, you
would usually prefer the Moore machine organization, even though it may
require more states. You should use edge-triggered flip-flops for the state
registers.
Synchronous Mealy machines can be constructed in TTL
logic, but the designer must be careful. The approach leads to more complex
designs that may affect the input/output timing of the FSM. You should use
asynchronous Mealy machines only after very careful analysis of the input/output
timing behavior of the finite state machine.
[Top] [Next]
[Prev]