INTRODUZIONE…cos’è una rete neurale?

SCOPO DEL NOSTRO LAVORO

RICERCA DELLA RETE MIGLIORE

ANALISI DEI DATI

CONCLUSIONI

Un normale calcolatore è in grado di compiere operazioni impensabili per un qualsiasi essere umano: esso è in grado di eseguire, per esempio, molti calcoli in successione in tempi brevissimi, ed è velocissimo nel fare cose complicate per la mente umana, come rotazioni di complesse figure geometriche, la memorizzazione di enormi quantità di dati etc...

Un normale calcolatore (che definiremo computer seriale) è costituito da un’unità di calcolo (processore) in grado di eseguire alcuni milioni di operazioni il secondo, e tre tipi di memoria: una contenente le istruzioni necessarie a svolgere le operazioni, una da cui vengono letti i dati da elaborare e depositati i risultati ed una permanente su cui i dati vengono registrati.

Il meccanismo di funzionamento di un calcolatore è grossolanamente questo: vengono letti sequenzialmente i dati e su di essi vengono applicate determinate operazioni predefinite dal programmatore.

Ogni dato viene allora elaborato singolarmente, e sottoposto ad una precisa sequenza di operazioni.

Proprio per questa ragione, un calcolatore tradizionale non è in grado di compiere operazioni che risultano semplicissime per la mente umana, come il riconoscimento di un oggetto in mezzo ad altri o la valutazione di un insieme di circostanze per prendere una decisione rapida.

La fondamentale differenza tra un calcolatore seriale e la mente umana sta nel fatto che mentre un calcolatore considera ed elabora in modo sequenziale un dato per volta, la mente umana elabora e valuta una gran quantità di informazioni contemporaneamente e la risposta all’ambiente è conseguente a tutte la stimolazioni che ogni singola informazione causa.

L’elaborazione delle informazioni avviene in parallelo.

Le reti neurali sono pensate e costruite secondo questo modello di elaborazione dati.

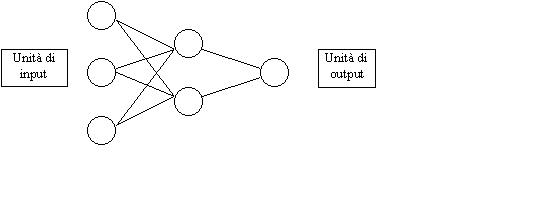
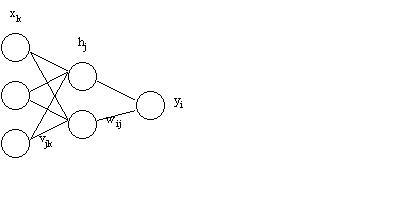
Una rete neurale è costituita da una serie di unità discrete (nodi o neuroni), connesse tra loro in modo da poter "scambiare" dei dati. Tipicamente sono presenti un certo numero di unità di input, in cui vengono inseriti i dati riguardanti l'evento da elaborare, un certo numero di unità nascoste (hidden) ed un certo numero di unità di output.

 I punti di connessione tra il collegamento (assone) e il nodo successivo sono dette sinapsi. Esse hanno la funzione di "pesare" l'informazione proveniente dal nodo precedente.

L'idea è quella di considerare un certo numero di variabili per descrivere un fenomeno (pattern di input). Il valore di tali variabili viene presentato ai neuroni di ingresso che rispondono alla stimolazione emettendo un segnale. Tale segnale giungerà, opportunamente pesato dai pesi sinaptici, alle unità successive che risponderanno alla stimolazione con un nuovo segnale.

Il processo si ripete finché il segnale non giunge alle unità di output, che daranno la risposta definitiva.

Evidentemente la risposta dipende dagli input e dai pesi sinaptici. Dobbiamo allora scegliere i pesi sinaptici in modo che la risposta sia "significativamente giusta". Sarà allora necessaria una fase d'allenamento in cui sono definiti i pesi sinaptici in modo da ottenere risposte il più vicino possibile a quelle desiderate.

Analizziamo il funzionamento più a fondo:

Supponiamo di mandare un segnale A in ingresso ad un neurone. Allora la risposta del neurone sarà:

,

dove F e detta funzione di attivazione. Normalmente, il neurone i-esimo ha una soglia di attivazione bi. Supponiamo che in ingresso al neurone i-esimo giungano i segnali xj provenienti dai neuroni precedenti pesati con i pesi sinaptici wij. Allora possiamo esprimere la risposta yi del neurone i-esimo in modo più corretto:

.

Parleremo più diffusamente delle funzioni di attivazione in seguito.

Se supponiamo , allora la formula della risposta assume un aspetto particolarmente semplice:

y = Wx -b.

L’apprendimento della rete avviene secondo precisi algoritmi che esprimono le modifiche da apportare ai pesi sinaptici in funzione della differenza tra la risposta fornita dalla rete e la risposta attesa per determinati patterns di input (patterns di allenamento). In fase di allenamento vengono presentati alla rete patterns con risposta nota. In base alla risposta si modificano i pesi sinaptici.

L’algoritmo più usato per la sua semplicità e potenza è il BACK PROPAGATION che verrà discusso in seguito.

Il tipo di risposta di ciascun neurone può essere diverso da rete a rete; tale tipo di risposta è regolato dalla funzione di attivazione.

I tipi di funzioni sono ovviamente infiniti, ma non tutti riescono a soddisfare certe necessità che si hanno nell’uso della rete.

Un esempio di risposta è quello della funzione a gradino

o analoga ma con output bipolare:

.

Questo tipo di funzioni però limita l’output a fornire solo un bit in uscita (acceso/spento) e non è quindi adatto nel risolvere problemi di una certa complessità: i neuroni necessari alla rete sarebbero troppi.

Una quantità di informazione maggiore può essere fornita da una funzione lineare:

con k costante e con opportune limitazioni dell’uscita per contenere il valore di attivazione del neurone.

La gradualità dell’attivazione del neurone consente una quantità di informazione molto maggiore.

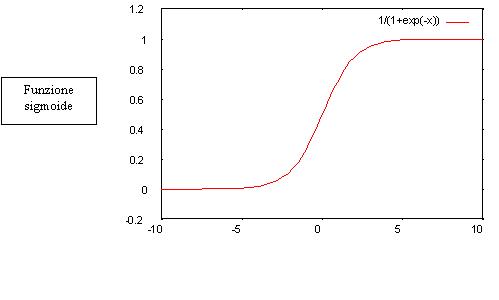
Nella rete da noi usata la funzione di attivazione (funzione sigmoide) non è di tipo lineare ma è data dalla equazione

che, con kà ¥, tende alla funzione gradino.

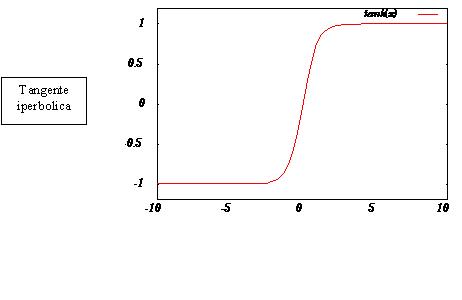
Analogamente, nel caso in cui volessimo un output bipolare, potremmo usare la funzione

i cui asintoti sono a –1 ed 1 (v. grafico).

Nella maggior parte dei modelli di rete, tratte che per i nodi di ingresso, si usano le stesse funzioni di attivazione per tutti i neuroni per calcolare il segnale in uscita.

L’algoritmo di Back-propagation non ha una data di nascita ben definita, la sua prima apparizione risale al 1969, ma la struttura è stata modificata innumerevoli volte adattandola al tipo di ricerca cui era destinata.

Il motivo per cui tanti ricercatori vi hanno speso il loro tempo modificandola è da ricercarsi nella grande versatilità, nella semplicità e nella potenza di tale metodo di apprendimento.

Il metodo di Back-propagation, infatti, è applicabile a qualsiasi rete multistrato, con un numero qualunque di connessioni ed è facilmente utilizzabile su reti con strutture molto disparate.

Il segreto di questo meccanismo sta nel metodo con cui la rete reagisce ogni volta che effettua un errore: tali errori vengono infatti propagati da ogni strato attraverso le connessioni sinaptiche e sommati per ciascuna unità da cui ricevono segnale.

Grazie a questo metodo, Back-propagation è molto efficace nel raggiungimento di risultati validi ed a generalizzare le soluzioni per esempi che non gli sono stati presentati durante l’addestramento.

Vediamo in dettaglio il suo funzionamento:

Per facilitare la comprensione, studiamo l’esempio della figura con le notazioni riportate.

Tutti i nodi sono attivati in modo non lineare tramite la funzione sigmoide , dove b è una costante positiva.

In ingresso viene fornito un pattern xm tramite il quale calcoliamo l’attivazione delle unità interne:

e analogamente quella delle unità di output:

.

Lo scopo della rete è naturalmente quello di minimizzare la differenza tra la risposta desiderata e quella fornita dalla rete stessa.

In formule la funzione dell’errore scelta (che deve essere minimizzata) è:

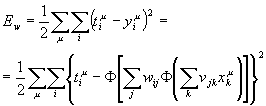
Per fare in modo che la rete si migliori, i parametri vengono fatti variare lungo la superficie dell’errore verso la direzione di massima pendenza negativa, applicando cioè quello che è definito come metodo di discesa del gradiente:

dove h rappresenta il "learning rate", e dove, ponendo si può semplificare così:

.

Il calcolo per la modifica delle connessioni inferiori è più complesso in quanto si deve tener conto della variazione delle unità interne rispetto a quella dei pesi sinaptici:

.

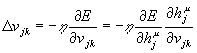La formula si sviluppa in modo del tutto analogo al caso precedente ottenendo:

.

Si noterà che nella formula dell’attivazione di ogni singola unità interna h_j è richiesta la somma dei prodotti tra i dello strato superiore ed i corrispondenti pesi sinaptici w_ij.

L’errore è, in altre parole, propagato all’indietro da uno strato a quello precedente.

Back-propagation, dunque, è un algoritmo piuttosto semplice da far eseguire ad un calcolatore ed è grazie a questo che è diventato il metodo più popolare tra gli studiosi di questo campo.

D’altra parte però tutto appare troppo bello per essere vero e, infatti, a tutta questa serie di vantaggi vanno considerati alcuni problemi nell’applicare tale metodo agli esperimenti.

Il primo è dovuto all’attivazione non lineare dei nodi che provoca un andamento assai complicato della funzione di errore: la superficie presenta un grande numero di minimi locali in cui la rete può restare "intrappolata" ed una serie di superfici piatte che rallentano l’apprendimento.

Il secondo problema riguarda invece la lentezza di tale algoritmo che può richiedere alcuni giorni per un singolo allenamento.

Come conseguenza sono state sviluppate molte varianti che mirano ad eliminare alcuni di questi problemi.

Riportiamo di seguito solo le modifiche che riguardano direttamente il nostro esperimento: il momentum e la tecnica detta Bold driver.

Il valore del learning rate ha nel back-propagation notevoli conseguenze: troppo piccolo implica lentezza e maggior rischio di finire in un minimo locale, troppo grande provoca oscillazioni eccessive sulla superficie dell’errore.

Per ovviare a questo problema si introduce una nuova variabile, il momentum, che consente un rapido spostamento nei punti della superficie dell’errore a pendenza molto bassa.

Questo permette di accelerare notevolmente l’apprendimento pur mantenendo un valore non troppo elevato del learning rate.

In pratica l’unica variazione consiste nell’aggiungere al calcolo della modifica della connessione, una frazione della modificazione ottenuta al passaggio precedente:

con a costante (momentum) e compresa tra 0 ed 1.

Il risultato è quello di accelerare l’apprendimento fino a dieci volte.

Il Dynamic Learning Parameters è un metodo che, oltre ad accelerare ulteriormente l’apprendimento, ha la capacità di diminuire la probabilità di capitare in un minimo locale.

Perché questo sia possibile si deve fare in modo che il learning rate sia grande inizialmente e decresca man mano che ci stiamo avvicinando alla soluzione.

Ci sono anche in questo caso molte tecniche diverse, quella da noi adottata è detta Bold driver.

Il metodo consiste nel far diminuire il valore del Learning rate nel caso che l’errore stia aumentando e nell’incrementarlo nel caso contrario:

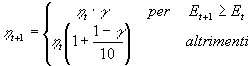
Il valore della costante g è stato fissato nel nostro caso pari a 0.999.

La rete neurale che abbiamo studiato è volta al riconoscimento di eventi in cui sono coinvolti antineutrini n e. Noi vogliamo che la rete sia in grado di riconoscere un evento interessante dal background. In pratica la rete deve essere in grado di riconoscere un positrone proveniente da una reazione in cui è coinvolto un dal rumore di fondo. Per fare questo sono state selezionate 16 variabili normalmente utilizzate per descrivere un evento di questo tipo: la rete le analizzerà, analizzerà le connessioni tra esse e "deciderà"se i dati presi in considerazione provengono da un evento interessante o no.

La rete ha 16 unità di input, 1 unità di output ed un numero di unità nascoste da ottimizzare. La funzione di attivazione dei neuroni è una sigmoide. L’output della rete sarà allora un numero y tale che:

0 £ y £ 1

In modo arbitrario decidiamo che un evento appartiene al segnale se l’output y è maggiore di 0.8:

y ³ 0.8

Le sedici variabili di input scelte sono:

1 - Plep: l’impulso del positrone

2 - Evis: l’energia totale visibile

3 - D Z = abs(Zvertex - Zelec)

4 - Pt,mis: impulso trasverso mancante

5 - xbjo: la x di Bjorken

6 - M: minima massa invariante tra il positrone candidato e tutte le altre

7 - pcon : contaminazione pionica nel TRD

8 - Phad: impulso adronico

9 - Eprs: l’energia depositata dall’elettrone nel preshower

10 - EOP

11 - f eh: angolo nel piano trasverso tra il positrone e l’impulso adronico

12 - f mh: l’angolo nel piano trasverso tra l’impulso adronico e l’impulso mancante

13 - Qt

14 - Qlep

15 - r: la coordinata radiale del vertice

16 - z: la coordinata lungo z del vertice

Per poter fornire un numero adeguato di pattern di sono necessari decine di migliaia di esempi.

Tali esempi vengono generati con una simulazione (montecarlo) degli eventi di segnale e di fondo.

Il campione di eventi montecarlo è diviso in tre tipologie: eventi di segnale, eventi di fondo da correnti cariche di n m , ed eventi di fondo di correnti neutre di n m .

Ognuno di questi campioni è diviso a metà: una parte è utilizzata per l’allenamento e l’altra per il test e la stima di efficienza e del fondo. In totale abbiamo sei file, tre per il training e tre per il test.

Il primo di ognuna delle due triplette di file tre file di ingresso contiene i dati per i quali la rete dovrebbe fornire una risposta positiva, gli altri due, al contrario, richiedono una risposta negativa della rete. L’allenamento si svolge con la presentazione alla rete di un evento preso dal primo, secondo e terzo file e così via, in successione. L’allenamento risulta allora ciclico. Tale ciclicità potrebbe influenzare la risposta della rete: spesso le regolarità introducono ciclicità nei calcoli della funzione d’errore alterando l’allenamento.

Verificheremo se il fatto di aver scelto questo tipo d’allenamento influenza o no la risposta della rete.

Come già discusso, la rete neurale in esame ha sedici neuroni di input ed un neurone di output. L'algoritmo di apprendimento che utilizziamo è BACK PROPAGATION con la modifica BOLD DRIVER.

L’utilizzo di BACK PROPAGATION comporta la scelta di due parametri: il learning rate iniziale (h) ed il momentum (a).

Il fatto di usare BOLD DRIVER, introduce un terzo parametro: il learning rate decrease (g), che noi considereremo fissato (g =0.999).

C'è inoltre un terzo parametro: il numero di nodi nascosti da utilizzare.

Il principale obiettivo che ci poniamo in quest’esperienza è quello di scegliere i tre parametri in modo da ottenere la rete che meglio si adatta al riconoscere eventi n e.

Faremo allora variare i nostri parametri in range abbastanza ampi, misureremo, per ogni terna di valori, l'efficienza (rapporto tra eventi "buoni" riconosciuti ed eventi "buoni" totali), il background (ovvero il rapporto tra il numero di eventi "cattivi" riconosciuti come "buoni" ed il numero totale di eventi "cattivi").

Si pone subito una questione decisiva: qual è la rete migliore? Quella con l’efficienza massima o quella con il fondo minimo? Oppure è meglio mettere in relazione questi due risultati e considerare per esempio il rapporto Efficienza/Background? Tenteremo di rispondere a questa domanda in seguito.

Ci sono poi altre cose interessanti da vedere: qual è la dipendenza della rete dai valori iniziali dei pesi sinaptici?

Prima di iniziare l’allenamento, noi assegniamo ai vari pesi sinaptici un valore casuale R, con:

R = Random -0.15 £ R £ 0.15

Supponendo di allenare più volte la stessa rete, fissati learning rate, momentum, numero di nodi nascosti, noi otterremo risultati diversi per efficienza e background, in quanto i pesi sinaptici iniziali saranno ogni volta diversi, in quanto casuali. Si tratta di valutare se questa "componente casuale" contribuisce all’interno dell’errore (ed è quindi trascurabile) o se contribuisce in modo sostanziale e bisogna valutarne gli effetti.

Possiamo poi provare a farci un’idea di qual è la reazione della rete all'eliminazione di una o più variabili di input: una delle caratteristiche di una rete neurale è appunto la "robustezza", ovvero la sostanziale indipendenza a piccole perturbazioni della sua struttura. Proveremo allora ad eliminare una, tre, cinque variabili di input sperando di mettere in luce da una parte un peggioramento delle prestazioni della rete all’aumentare delle variabili eliminate, dall'altra una maggiore importanza di alcune variabili rispetto alle altre.

Le reti neurali che sono usate nella realtà non sono come quelle descritte, costituite da reti di neuroni, ma sono in realtà simulazioni di queste generate da normali calcolatori seriali.

Per eseguire tali simulazioni esistono programmi appositi, uno dei quali, quello da noi usato, è Jetnet 3.0, un programma in Fortran messo a disposizione dal CERN ed ottenibile via ftp tramite Internet.

Per simulare una rete usando tale programma è necessario scriverne un altro in Fortran che richiami quando servono le routine contenute in Jetnet.

Il programma non è quindi altro che un insieme di procedure che però non possono essere gestite da sole, ma necessitano di un altro programma esterno che decida quali sono necessarie ed in quale ordine.

Il programma che durante il nostro esperimento ha assolto la funzione d’interfaccia per Jetnet si chiama Elenet.

Si tratta anche in questo caso di un programma in Fortran (come esplicitamente richiesto dal manuale di Jetnet) che era stato precedentemente scritto da Roberto Renò.

Una volta che il programma era compilato ed eseguito, appariva una schermata tramite la quale si poteva scegliere la funzione da eseguire: allenamento, test, applicazione ai dati per vari esperimenti con diverse particelle.

Durante l’esperimento però, come vedremo, abbiamo riscontrato l’impossibilità di utilizzare tale programma senza modifiche in quanto era necessario che ciascuna delle funzioni sopra dette fosse eseguita moltissime volte ciclicamente.

Il programma originale dunque è stato modificato più volte, adattandolo alle necessità che si riscontravano durante l’esperimento, tramite l’inserimento ove necessario di cicli che automatizzavano la ripetizione di determinate funzioni, evitandoci così ore di lavoro ripetitivo e meccanico.

Man mano che spiegheremo le varie fasi dell’esperimento verranno anche chiarite in parte le modifiche che è stato necessario apportare al programma originale.

Lo scopo della nostra ricerca è quello di trovare, fra varie combinazioni di parametri iniziali nell’apprendimento, quale consente di ottenere la rete "migliore".

Il significato del concetto di "migliore" dipende dalle applicazioni che si intende eseguire con la rete da noi sviluppata: secondo i casi può essere necessario avere un’efficienza di risposta molto alta, senza tenere troppo in considerazione se il fondo (ovvero il numero delle misure che la rete ha interpretato male) aumenta o l’esatto contrario.

Noi abbiamo ritenuto più opportuno considerare migliore una rete "intermedia" tale cioè da avere il massimo rapporto tra efficienza e fondo. Ciò non toglie che per determinate applicazioni possa essere necessario optare per una scelta diversa.

Chiarito questo passiamo ad analizzare le variabili che abbiamo fatto variare e la scelta dei range di variazione per ciascuna di queste variabili.

Uno dei parametri avrebbe potuto essere il learning decrease rate (g ) che controlla la variazione del learning rate per il metodo del Bold Driver dopo la presentazione di ciascun pattern di addestramento.

Abbiamo però deciso di non far variare tale variabile e di mantenerla costante al valore g = 0.999 in quanto, per non provocare eccessive oscillazioni e casualità nei risultati è necessario mantenerla molto vicina ad 1.

Discorso analogo vale per il limite superiore del valore dei pesi iniziali: tale valore viene inserito come parametro in Jetnet e costituisce il valore massimo che i pesi iniziali possono assumere nella scelta casuale iniziale.

Esiste una formula empirica 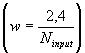per tale valore che dà come risultato

w » 0.15,

nonostante ciò abbiamo deciso di effettuare prove con valori più alti di w col risultato che le risposte della rete erano fortemente casuali: eseguendo più volte lo stesso allenamento lasciando invariati gli altri parametri, infatti, le variazioni che si ottenevano per efficienza e fondo da una prova all’altra erano superiori all’errore del calcolo di tali variabili.

Come conseguenza abbiamo deciso di lasciare invariata anche questa variabile evitando che valori troppo alti di questa falsassero il risultato.

I parametri che, al contrario, abbiamo fatto variare sono:

• Learning rate (h )
• Momentum (a )
• N° di unità nascoste

vediamoli in dettaglio:

Come già notato in precedenza, la scelta del valore del learning rate è piuttosto delicata: un valore alto rallenterebbe notevolmente l’addestramento ed aumenterebbe il rischio di rimanere in un minimo locale della funzione d’errore, parallelamente, un valore troppo elevato comprometterebbe la capacità di convergere ad un minimo dell’errore.

Di conseguenza, empiricamente si è posto di assegnare a tale parametro un valore non superiore ad 1.

Attenendoci a questa norma abbiamo inizialmente fatto in modo che il valore di h variasse nel range

0 < h < 1,

con 0.1 di passo.

Durante l’analisi dei dati ci aspettavamo che, al variare di h , il rapporto efficienza/fondo salisse fino ad un certo valore per poi ridiscendere ma, al contrario questo risultava salire costantemente.

Stupiti da tale comportamento abbiamo valutato la possibilità di portare il learning rate a valori superiori ad 1: dato infatti che alla nostra rete è applicato il metodo Bold Driver che abbassa il valore di h man mano che ci si avvicina al risultato, niente vieta che inizialmente tale valore superi il canonico 1, anche se in realtà questo può provocare salti iniziali eccessivi sulla superficie dell’errore aumentando la casualità dei risultati.

Abbiamo quindi optato per il range

0 < h < 2

sempre con un passo di 0.1.

Come vedremo, il risultato è stato in effetti proprio quello previsto: al salire del valore di h i dati hanno variazioni regolari finché il fatidico 1 non viene superato.

Per questa variabile il valore deve essere minore di 1, la scelta perciò del range di variazione è stata molto più semplice:

0 < a <1

con passo pari a 0.1.

Il numero di unità nascoste è un parametro molto importante per la rete in quanto, mentre un numero esiguo di nodi interni pregiudicherebbe la possibilità di risolvere il problema, un numero eccessivo provocherebbe, a parità di prestazioni, un aumento rilevante dei tempi di addestramento.

Di conseguenza abbiamo scelto un range abbastanza alto di variazione:

9 £ N £ 51

tale da garantirci risultati utili.

In realtà, come vedremo, tale parametro non influenza in modo rilevante il risultato, probabilmente si tratta di un problema non molto complesso da risolvere per una rete neurale, tanto da non richiedere un numero eccessivo di connessioni sinaptiche.

La ricerca della rete migliore ha richiesto numerosi giorni di lavoro ad un calcolatore piuttosto potente situato a Ginevra, la mole di operazioni richieste è stata in effetti enorme ed il file con i risultati ottenuto contiene 8170 righe di dati, ciascuna corrispondente ad una rete testata.

Per ottenere tale risultato è stato necessario modificare Elenet introducendo tre cicli in cascata per ciascuna variabile da analizzare in modo tale che, per ogni combinazione di questi, la rete venisse reinizializzata e fossero eseguiti il training ed il test.

Come già discusso, abbiamo "informatizzato" questa parte dell’esperienza inserendo tre cicli all’interno del programma "Elenet" scritto da Roberto Renò. Abbiamo fissato i seguenti range di variazione:

Per ogni tripletta di valori delle tre variabili, Elenet ha effettuato tramite Jetnet l’allenamento della relativa rete e poi il test. I risultati del test (efficienza della rete e background con relativi errori) sono stati scritti dal programma in un file.

Sono state effettuate complessivamente 8170 misure di efficienza e fondo su altrettante triplette di valori.

Abbiamo costruito gli istogrammi per il fondo, per l’efficienza e per il rapporto. Si notano delle distribuzioni piccate attorno ad un valore medio. Le distribuzioni indicano quindi un valore "preferito" medio con una certa incertezza.

Vediamo però di rendersi meglio conto di cosa indicano i risultati.

I valori medi per l’efficienza (e ) ed il background (b ) sono:

e _m = 31.1% b _m = (1.3 * 10^-2) %

In accordo con le considerazione fatte in precedenza, abbiamo deciso di considerare il rapporto efficienza/background come indicatore significativo della "bontà" della rete. Abbiamo allora creato un algoritmo in grado di cercare la tripletta di parametri per cui tale rapporto era massimo.

Abbiamo allora operato dei tagli alle distribuzioni dei risultati, richiedendo che l’efficienza ed il fondo cadessero entro un intervallo da noi stabilito. Questo è stato fatto per evitare di considerare dati molto lontani dal valor medio con uno scarso significato fisico.

Le richieste sono allora:

Con questi tagli, la rete migliore risulta essere:

con i seguenti risultati:

Ovviamente ha poco senso parlare di tripletta migliore, in quanto ci sono molte alte triplette che danno risultati identici all’interno dell’errore.

Notiamo subito che l’efficienza è più alta del valor medio. Notiamo anche che le reti con i più alti R sono quelle caratterizzate da fondo basso.

Il perché di questo fatto risulta chiaro una volta esaminati i range di variazione di efficienza e fondo: le oscillazioni del fondo sono molto più ampie, percentualmente, di quelle dell’efficienza.

In altre parole, la distribuzione del fondo è molto più larga di quella dell’efficienza: la quantità di eventi che compare nel calcolo dell’errore del background è molto minore di quella per il calcolo dell’errore per l’efficienza.

Quando calcoliamo il rapporto di conseguenza, i risultati con fondo minore sono ovviamente quelli a fondo più basso.

Come già discusso, la scelta della rete migliore resta fortemente legata al tipo di utilizzo che il ricercatore intende fare: si può essere interessati ad un efficienza alta senza preoccuparsi del fondo, oppure ad un fondo basso, con un efficienza limitata.

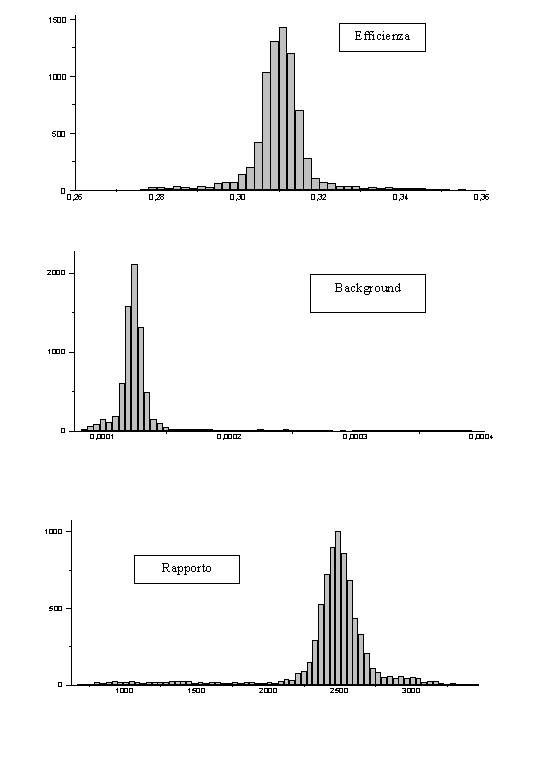
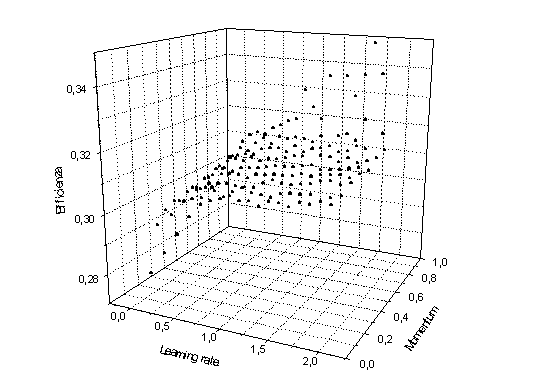
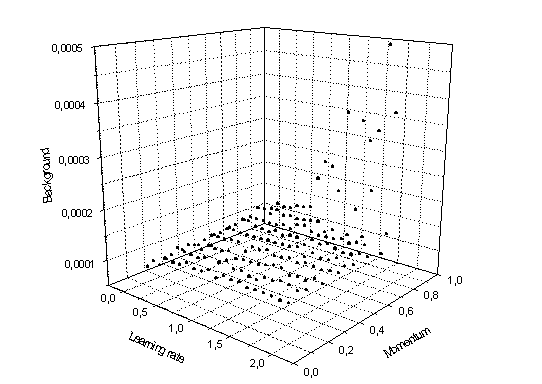
Riportiamo l’andamento qualitativo di efficienza e fondo in funzione di learning rate e momentum per una rete con 43 nodi nascosti:

- Analisi del comportamento al variare dei singoli parametri.

Per renderci meglio conto di "quanto conta" la variazione del singolo parametro, prendiamo come indicativi i risultati ottenuti sopra nella ricerca del rapporto massimo, fissiamo volta per volta due dei tre parametri e vediamo il comportamento della rete al variare del terzo.

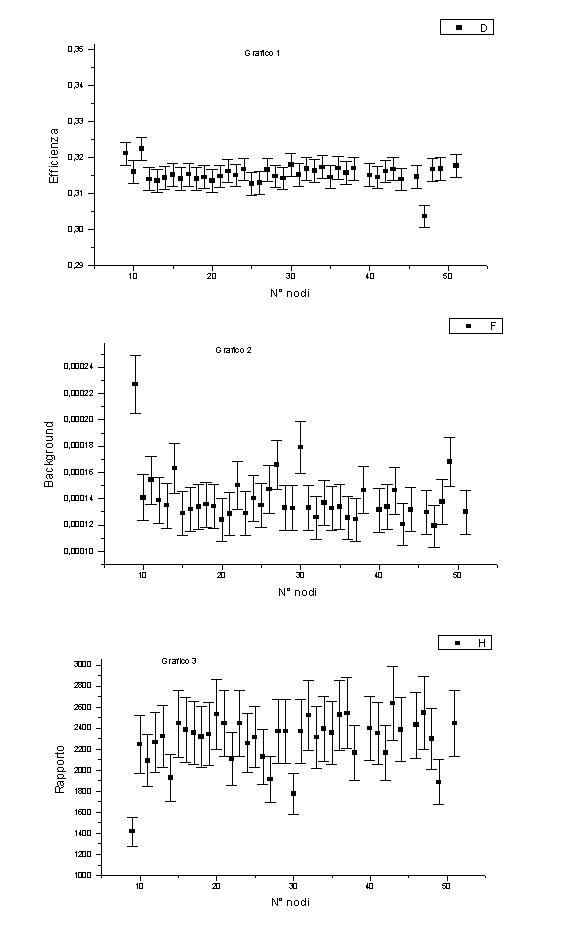
Fissiamo allora h = 1.4 e a = 0.8. Vediamo il comportamento della rete al variare del numero di nodi (grafici 1, 2 e 3).

L’andamento di efficienza, background, rapporto è sostanzialmente casuale, non si notano regolarità. Le oscillazioni avvengono attorno ai dei valori medi e sono sostanzialmente all’interno dell’errore. Da notare che l’oscillazione sul background (più consistente di quella sull’efficienza) fa oscillare fortemente il rapporto. La rete a 43 nodi è quella che ha il background più basso.

Il comportamento della rete è allora da considerarsi indipendente dal numero di unità nascoste (nel range di variazione da noi scelto).

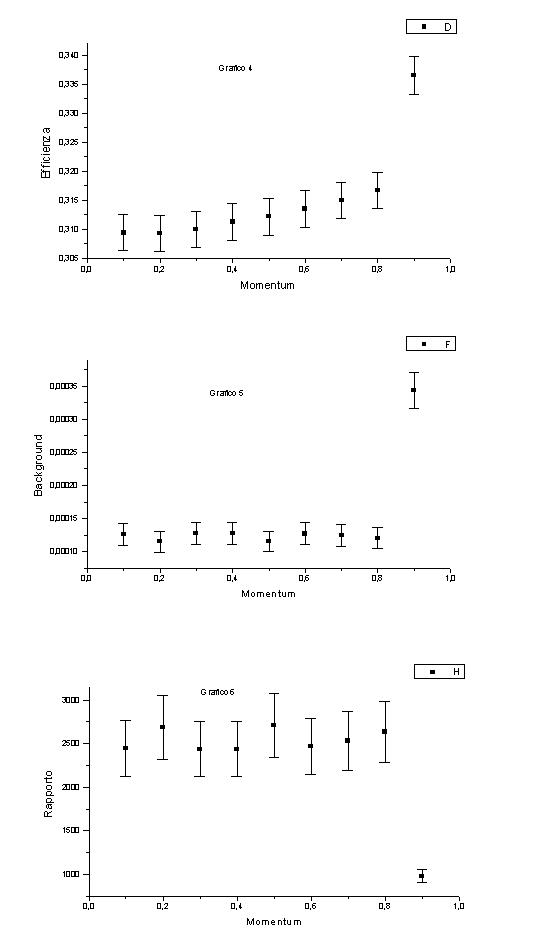
Fissiamo h = 1.4 e n (numero di nodi) = 43 (grafici 4,5 e 6).

Al variare del momentum succedono cose interessanti: l’efficienza aumenta in modo regolare all’aumentare del momentum. L’andamento del background è analogo (più oscillante). Sia l’efficienza che il background hanno un picco per a = 0.9, ma il picco del background è molto più alto (in percentuale): il fondo passa infatti da valori intorno a 1.3*10^-4 a 2.2*10^-4, mentre l’efficienza passa da valori intorno a 31.3% a 33.7 %.

Il risultato è che il rapporto è governato dalle oscillazioni ed presenta un minimo per a = 0.9.

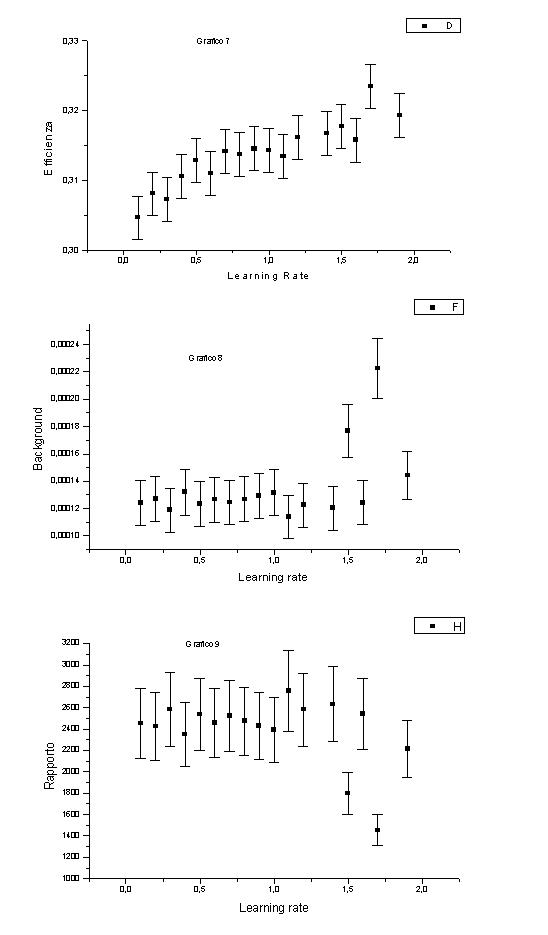
Fissiamo a = 0.8 e n = 43 (grafici 7,8 e 9).

Notiamo che l’efficienza sale con regolarità finché h < 1. Poi la tendenza è ancora a salire, ma con grosse oscillazioni.

Sul fondo si ha un andamento analogo (regolare, più oscillante, se h < 1, fortemente irregolare se h > 1).

Questo porta ad un andamento del rapporto regolare (comunque pilotato dalle oscillazioni del fondo) se h < 1 , estremamente oscillante altrimenti.

Evidentemente le triplette con h > 1 creano problemi in fase d’allenamento e test.

I casi con h > 1 sono inusuali, ma, come già discusso, non sono neppure esplicitamente proibiti, soprattutto nel caso di algoritmo "bold driver", che modifica h in corso d’opera.

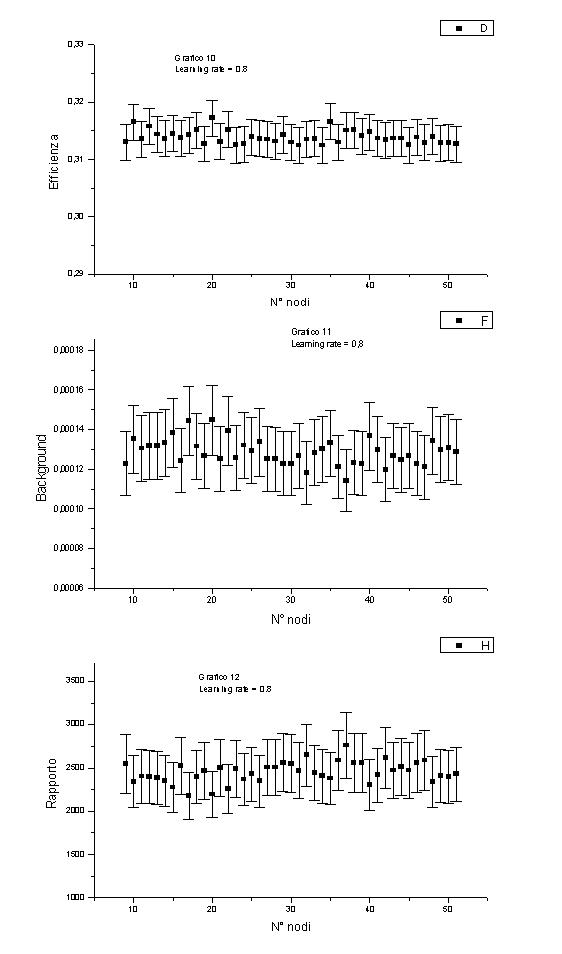
Abbiamo allora ripetuto la precedente analisi con h = 0.8.

I risultati relativi alla tripletta (h = 0.8, a = 0.8, n = 43) sono :

e sono compatibili entro l’errore con quelli della rete migliore.

Fissiamo h = 0.8 e a = 0.8 (grafici 10,11 e 12).

Non ci sono differenze sostanziali da quanto discusso prima.

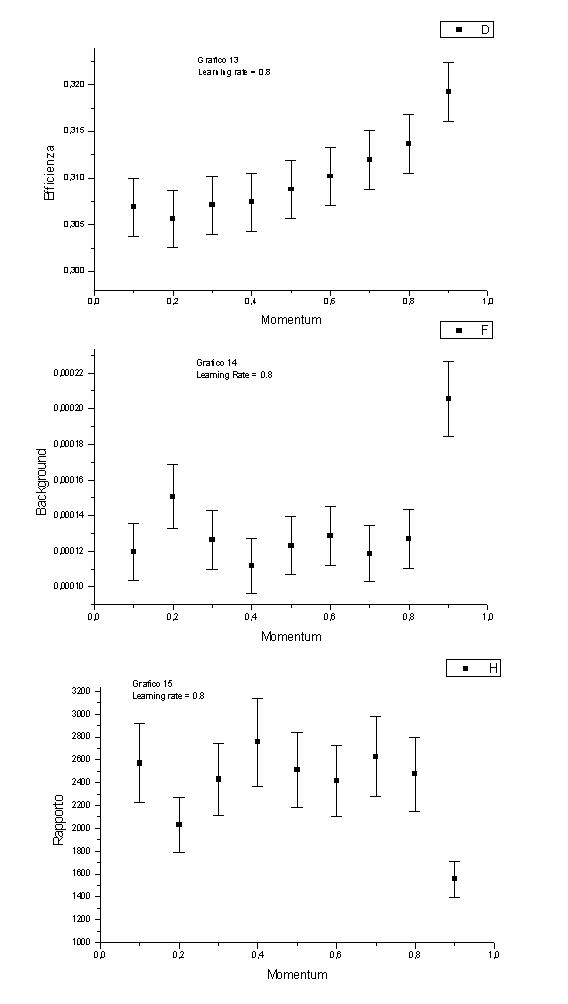
Fissiamo h = 0.8 e n = 43 (grafici 13,14 e 15).

L’efficienza ha un andamento regolare, ancora più regolare di prima (cresce al crescere del momentum).

Il background rimane oscillante, quindi il rapporto è oscillante.

Siamo quindi riusciti a mettere in luce alcuni aspetti importanti :

• La nostra rete è sostanzialmente indipendente dal numero di unità nascoste (se il numero è compreso tra 9 e 51). Dovendo costruire realmente una rete neurale, opteremmo per una rete con pochi nodi nascosti, in quanto più economica e più veloce da allenare.
• L’efficienza della nostra rete cresce al crescere del momentum in modo regolare. Dovremo allora scegliere a = 0.9 se il nostro obbiettivo fosse di ottenere un alta efficienza. A causa delle oscillazioni sul fondo, però, la regolarità dell’andamento dell’efficienza non si ripercuote sull’andamento del rapporto.
• L’efficienza della nostra rete cresce al crescere del learning rate. Valori del learning rate maggiori di uno sono permessi ma sconsigliati perché causano forti oscillazioni su efficienza e fondo. Il comportamento della rete è meno regolare e difficilmente controllabile. Risulta allora ottimale un h = 0.9 o h = 1 nel caso in cui si sia interessati ad un’alta efficienza. Anche in questo caso il rapporto risulta oscillante e poco significativo.

Prima dell’inizio dell’allenamento della rete neurale, i valori di tutti i pesi sinaptici iniziali w_ij vengono generati in modo random. Sono quindi casuali. Nel nostro caso

Ci interessa ora valutare se questa componente casuale influenza la risposta della rete, se ne dobbiamo tenere conto nel valutare i nostri risultati.

Per fare questo è stato sufficiente inserire un ciclo nel programma Elenet in modo da ripetere molte volte l’allenamento con learning rate, momentum, nodi nascosti fissati. Infatti i numeri random utilizzati per settare i pesi sinaptici iniziali non sono poi così random: il computer ha una "lista" di numeri in memoria e legge i numeri in successione. Quindi, se il programma gira molte volte, verranno letti molti numeri random diversi.

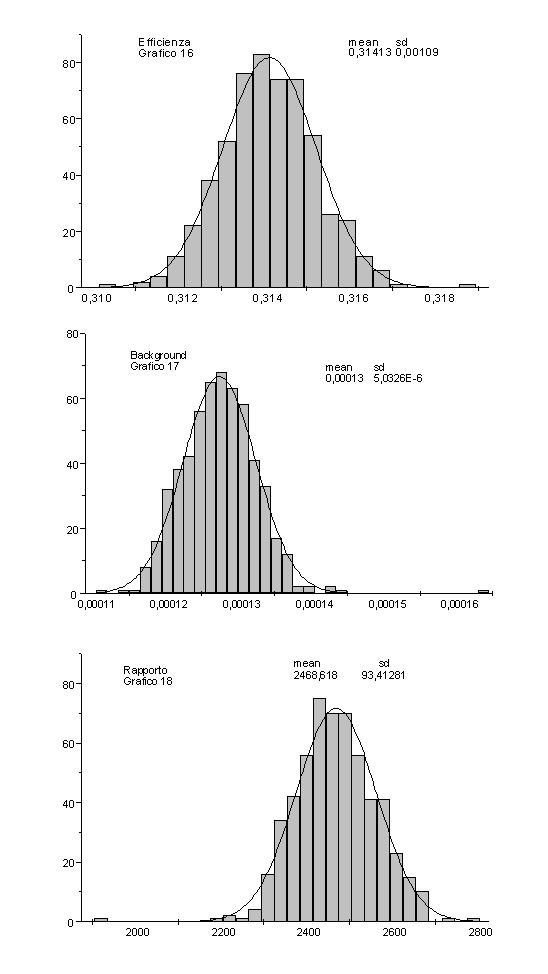
Abbiamo fissato h = 0.8 , a = 0.8 , n = 43 ed abbiamo effettuato tale misura.

Gli istogrammi relativi alle distribuzioni di efficienza, fondo e rapporto sono gli istogrammi 16,17 e 18. Una volta effettuato il fit gaussiano abbiamo ottenuto:

ovvero, prendendo come errore una deviazione standard, si ottiene

Per background e rapporto si ottiene:

Background : mean = 0.00013 sd = 5.0326E-6

Rapporto: mean = 2468.61853 sd = 93.81564

ovvero

I risultati che avevamo ottenuto per h = 0.8 , a = 0.8 , n = 43 erano:

Concludiamo quindi che l’effetto della variazione casuale dei pesi sinaptici iniziali è trascurabile, in quanto le distribuzioni ottenute, fittate con gaussiane, hanno deviazione standard minore dell’errore ottenuto per via algebrica associato alle misure effettuate nella ricerca della rete migliore.

Una caratteristica peculiare di una rete neurale è la "robustezza", ovvero la capacità di fornire una risposta esatta anche se sono state apportate lievi modifiche alla sua struttura. Per un normale calcolatore seriale, questa proprietà è inesistente: quando il calcolatore non è in grado di eseguire una delle operazioni necessarie al raggiungimento del risultato, si blocca. Infatti, in un processo, seriale non è possibile "saltare" un passaggio.

Per quanto riguarda una rete neurale, invece, la situazione è molto diversa. Supponiamo, per esempio, che ad una rete manchi una delle informazioni d’ingresso: la rete elaborerà le rimanenti informazioni e darà una risposta lo stesso. Se la modifica (che può essere causata da rumore, danneggiamento o altro) è di lieve entità, la rete è comunque in grado di lavorare e di fornire risposte corrette. L’analogia con i sistemi biologici (per esempio il cervello umano) è stringente: se il cervello umano subisce dei danni parziali, è comunque in grado di assolvere alle sue funzioni. Se, a causa di lesioni, una persona diventasse cieca, sarebbe ugualmente in grado di riconoscere, per esempio, una mela grazie al tatto, al gusto, all’odorato.

Abbiamo allora provato allora a fare tre tipi di misure: abbiamo posto a zero (sia nell’allenamento che nel test, ovviamente) una, tre, cinque variabili di input.

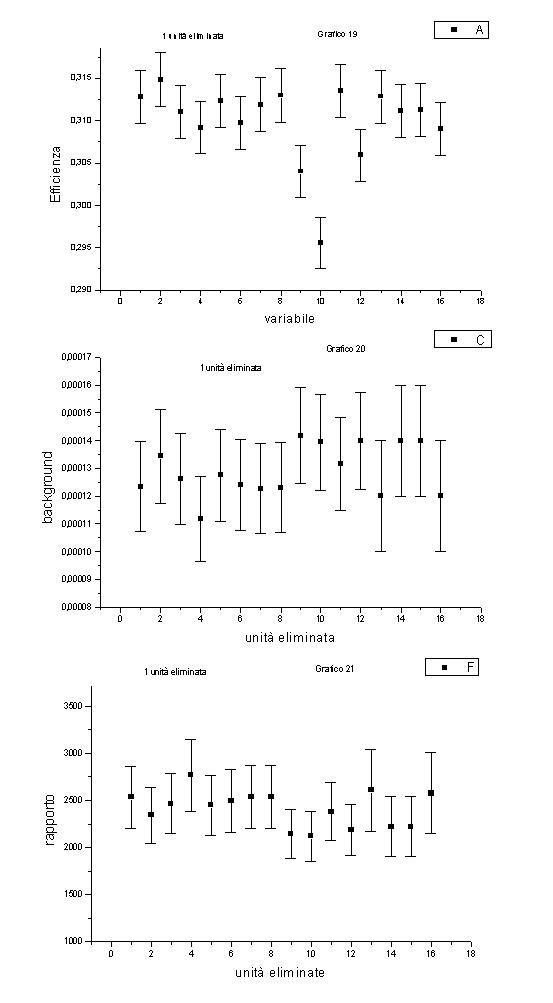
Per quanto riguarda l’eliminazione di una variabile, abbiamo inserito un ciclo (abbiamo inserito la variabile p, che varia da 1 a 16 con step 1 ed abbiamo posto a zero la variabile p-esima) in Elenet che elimina le sedici variabili in successione, una per volta.

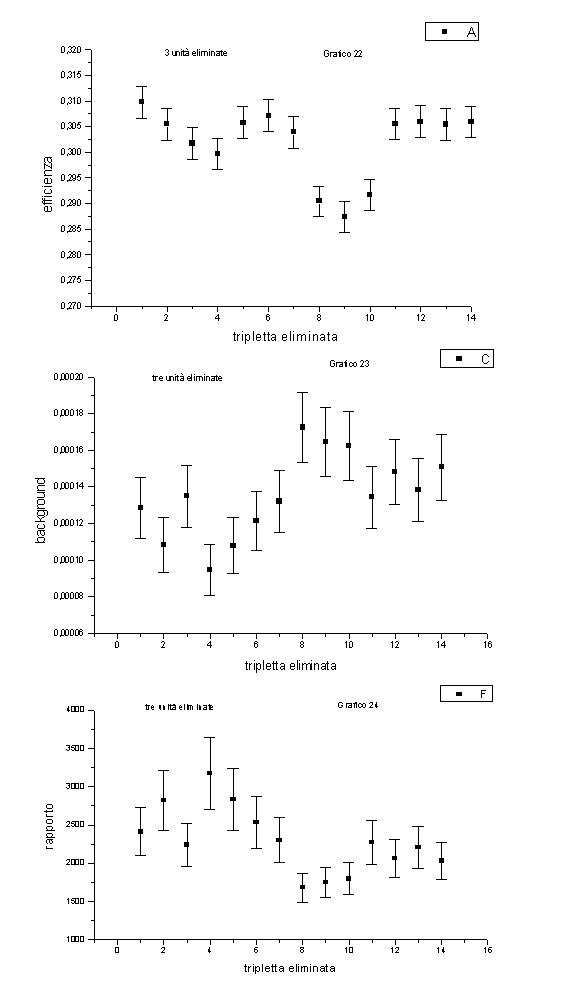
Per l’eliminazione di tre (cinque) variabili, abbiamo mantenuto lo stesso ciclo richiedendo che fossero eliminate tre (cinque) variabili consecutive (per quanto riguarda le tre variabili, abbiamo fatto variare p tra 1 e 14 ed abbiamo posto a zero le variabili p-esima, (p+1)-esima, (p+2)-esima, per cinque variabili analogo).

In questo modo si dovrebbe mettere in luce da una parte un peggioramento progressivo delle prestazioni della rete, dall’altra una maggiore importanza di alcune variabili rispetto alle altre.

Abbiamo fissato h = 0.8 , a = 0.8 , n = 43.

I grafici relativi a questa parte dell’esperienza sono numerati da 19 a 27.

Notiamo intanto che le efficienze e i rapporti diminuiscono progressivamente all’aumentare del numero di variabili eliminate, mentre il background aumenta. Riportiamo (giusto per visualizzare questo fatto, in realtà queste medie non hanno senso fisico) le medie di efficienza, fondo e rapporto sulle misure fatte:

L’andamento generale dei dati è quindi quello atteso: la rete peggiora le sue prestazioni (soprattutto per quanto riguarda l’efficienza) man mano che aumenta il numero di unità eliminate.

Possiamo però provare a dire qualcosa di più: guardando il grafico 19, dove è graficata l’efficienza in funzione del numero della variabile eliminata, notiamo delle cadute di efficienza all’eliminazione della variabile 10 (EOP), 9 (E_prs) e 12 (f _mh). Possiamo allora supporre che tali variabili siano risultate particolarmente significative per il riconoscimento degli eventi buoni.

Andando a guardare cosa succede al rapporto (grafico 21), notiamo che il rapporto risulta essere basso per le variabili 9, 12, 10, ma anche 13 (Q_t) e 14 (Q_lep), tutte variabili che Roberto Renò ci ha confermato essere variabili importanti nell’analisi standard, e quindi importanti nel riconoscimento di un evento buono.

Passiamo ad analizzare i dati ottenuti eliminando tre variabili consecutive.

Dal grafico 22 (efficienza in funzione della tripletta eliminata), notiamo che le triplette ad efficienza più bassa sono i numeri 8,9 e 10, che sono quelle che coinvolgono la variabile EOP (ricordarsi che al ciclo p-esimo abbiamo eliminato le variabili p-esima, (p+1)-esima, (p+2)-esima). L’analisi del grafico 24 (riguardante il rapporto) ci conferma che la variabile EOP è stata riconosciuta come importante dalla rete neurale.

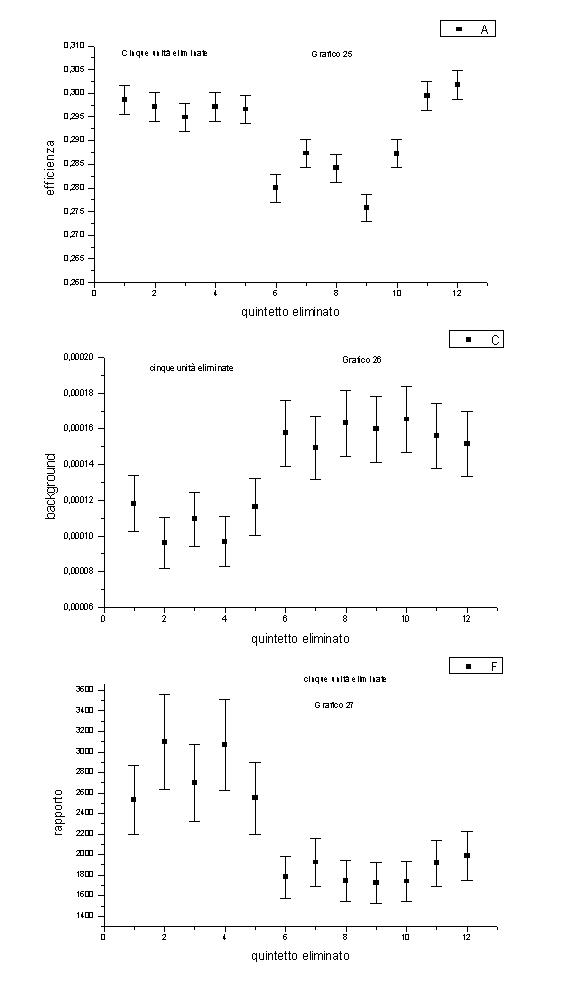
I grafici riguardanti cinque variabili eliminate (grafici da 25 a 27) mostrano efficienze e rapporti bassi per i quintetti che coinvolgono EOP e f _mh (o entrambe): notiamo infatti che i quintetti 6-12 hanno efficienze (ma soprattutto rapporti) bassi.

Concludiamo allora che la variabile EOP riveste un’importanza particolare nel riconoscimento degli eventi "buoni". Anche altre variabili si sono rivelate importanti (per esempio f _mh).

Per contro, alcune variabili che ci aspettavamo essere importanti non si sono rivelate vitali per il funzionamento della rete: è il caso di P_t,mis o di M (impulso trasverso mancante e minima massa invariante tra il positrone candidato e tutte le altre, rispettivamente variabili 4 e 6). Bisogna però tenere conto del fatto che la rete non valuta la singola variabile, ma le connessioni con le altre variabili in ingresso, ed è quindi difficile, o quantomeno non ovvio, prevedere quali connessioni rivestono particolare importanza e risalire quindi a quali variabili sono vitali e quali no.

Nell’Elenet originale e per la maggior parte dei nostri esperimenti, i pattern di ingresso sono stati forniti con un ordine preciso: uno per il quale ci aspettavamo una risposta positiva (1) e due cui viceversa la risposta attesa era negativa (0).

E’ possibile che la rete interpreti male questa ciclicità e che l’apprendimento venga in qualche modo falsato?

L’efficienza riscontrata intorno al 30% in effetti può avvalorare la tesi di un errore di procedura: la rete infatti risponde correttamente una volta su tre perché questo è il suo limite o perché ha in qualche modo imparato a rispondere in modo ciclico?

Per controllare questo fatto abbiamo di nuovo modificato Elenet in modo che i dati in ingresso fossero forniti a Jetnet in ordine casuale ed abbiamo poi ripetuto più volte l’apprendimento per la rete col massimo rapporto efficienza/fondo.

Ecco gli istogrammi relativi ai dati ottenuti:

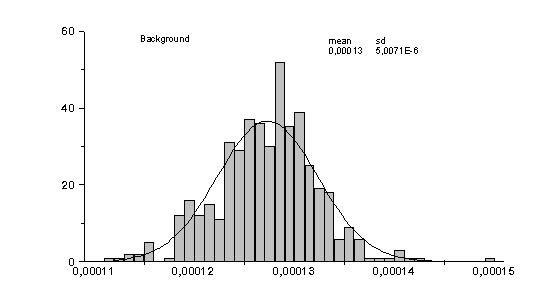
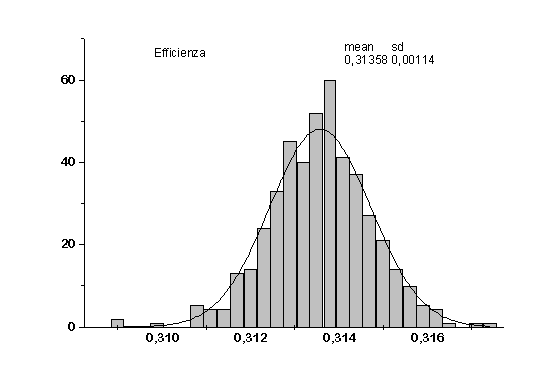
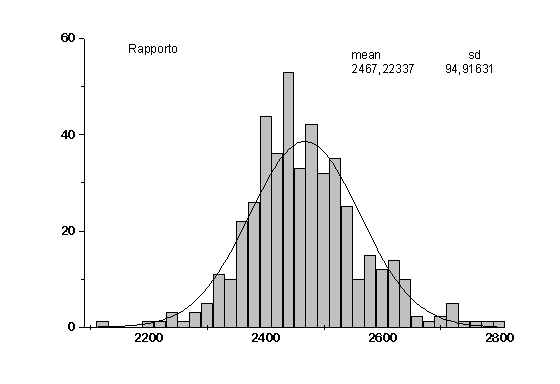
Il risultato di questa analisi è che le variazioni riscontrate sono rimaste nell’errore di misura delle risposte: la rete non si "accorge" della cambiamento effettuato e l’output quindi non dipende sostanzialmente da come vengono forniti i dati in ingresso.

Cerchiamo di riassumere quanto abbiamo sperimentato:

La risposta di una rete neurale a 16 nodi d’ingresso è funzione (oltre che dei valori delle 16 variabili di input) del valore del learning rate, del momentum, del numero di nodi nascosti, del valore iniziale dei pesi sinaptici.

Il nostro compito era di mettere in evidenza eventuali dipendenze dell’output della rete da questi parametri.

Innanzitutto, misurando efficienza, fondo e rapporto efficienza/fondo su tutte le possibili triplette di valori del learning rate, momentum, nodi nascosti, (entro limiti da noi stabiliti) abbiamo messo in luce una stretta dipendenza dell’efficienza dal momentum e dal learning rate: l’efficienza aumenta all’aumentare di questi due parametri. Ci siamo allora posti il problema dell’opportunità di scegliere learning rate maggiori di uno, abbiamo effettuato le misure necessarie, evidenziando un andamento fortemente irregolare dell’efficienza. Reti con h > 1 sono dunque permesse (almeno con il nostro algoritmo di apprendimento) ma sconsigliate.

La risposta della rete risulta invece essere indipendente dal numero di nodi nascosti. Abbiamo attribuito questo ad una sostanziale semplicità del problema da risolvere.

Il fondo è pressoché indipendente dai parametri presi in esame. Ha un andamento fortemente irregolare per ogni valore dei parametri.

Considerata questa irregolarità del fondo e la regolarità dell’efficienza, non ci stupiamo nello scoprire che il rapporto è fortemente oscillante, e indipendente dai parametri.

Per quanto riguarda la dipendenza della rete dai pesi iniziali, effettuate le misure necessarie, abbiamo visto che il contributo di questa componente casuale è all’interno dell’errore, ed è quindi trascurabile.

Abbiamo poi eliminato una, tre, cinque unità di input ed abbiamo notato un peggioramento progressivo delle prestazioni della rete (come atteso). Abbiamo inoltre messo in luce una particolare importanza della variabile EOP nel riconoscimento degli eventi interessanti. Si nota inoltre che alcune variabili importanti nell’analisi standard non rivestono particolare importanza per la nostra rete neurale: la rete studia le connessioni tra le variabili e non la singola variabile. Non ci stupiamo allora se alcune variabili ritenute fondamentali non si rivelano tali all’interno della rete.