Our lab and experiments

Controlling atomic matter waves by shaking them

Quantum particles tunneling between the sites of a periodic lattice can be made to slow down, stop or turn around by shaking the lattice back and forth. This simple method suggests a new kind of quantum control and the creation of “dressed matter waves”.

Apparently simple and well-understood physical systems can show surprising behaviour under certain circumstances, especially when they are strongly driven from the outside. Take, for instance, a simple rigid pendulum. Its bob will swing back and forth sinusoidally if it is slightly displaced from its downward equilibrium position. If we now hold its pivot and shake it up and down, this simple swinging motion can be radically modified, and for some particular frequency and amplitude of the shaking the pendulum can even invert its equilibrium position and start oscillating with its bob above the pivot rather than below it (1) (see Figure 1). This surprising behaviour also carries over into the quantum world. In quantum physics, one of the key processes without an analogue in the classical world is tunneling.  A quantum particle - an atom, for instance - trapped in a potential well can “tunnel” through a classically forbidden barrier into an adjacent well and back again (Figure 2(a)), giving rise to a to-and-fro motion reminiscent of a pendulum's swinging motion. If the wells are now shaken back and forth (or, alternatively, an oscillatory force is applied to the particle), the tunneling of the particle is modified: its amplitude can be reduced or even completely suppressed as shown in Figure 2(a) (2,3), and for certain parameters of the shaking the particle's quantum mechanical phase can be inverted in the process (which corresponds to the classical pendulum's swinging upside down). This principle can also be extended to a series of potential wells forming a periodic lattice structure.  A particle trapped in one of the wells can be prevented from tunneling into neighbouring wells by an appropriate choice of the frequency and amplitude of the shaking (Figure 2(b)).  This phenomenon, which was initially proposed as a method for  controlling the propagation of excitons in insulating crystals (4),  is known as “dynamical localization”(5).



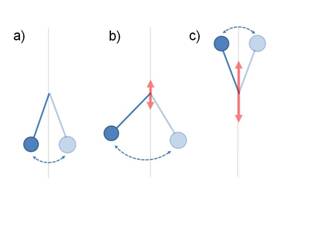
FIGURE 1: When a simple pendulum (a) is strongly driven by shaking its pivot up and down, its dynamics can be substantially modified (b) up to the point where the pendulum oscillates upside-down, with the bob above the pivot (c).




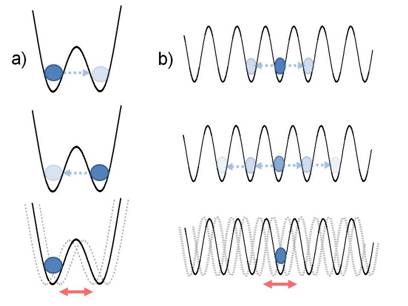
FIGURE 2: The tunneling of a quantum particle between two potential wells can be suppressed by shaking the wells back and forth (a). In the same way, a particle can be prevented from spreading inside a periodic potential (b).

Atoms in artificial crystals

Over the past two decades it has become possible to study the quantum dynamics of particles in periodic potentials using ultra-cold atoms trapped in laser-induced standing waves, so-called optical lattices (6,7). Essentially, one starts with a gas of atoms at room temperature, cools them down to a few billionths of a dgree above absolute zero (using a combination of laser cooling and evaporative cooling techniques) and then traps the atoms with crossed laser beams that create a “light crystal”. In this way, it is possible to mimic the dynamics of electrons in crystal lattices, but with the added advantage that one has full control over the geometry of the lattice and can even “look inside” the crystal by simply switching off the laser beams that create it in the first place. Using these (and some other) tricks we were able directly to observe dynamical localization in the laboratory.

In our experiments we achieved a situation that closely resembles the idealized depiction in Figure 2(b). After creating an extremely cold cloud of rubidium atoms (so cold, in fact, that – very simply speaking - they all occupied the lowest possible energy level of the laser trap, thus forming a Bose-Einstein condensate) we switched on a laser beam that was retro-reflected by a mirror and gave rise to a one-dimensional standing wave at the position of the rubidium atoms. This standing wave, in turn, resulted in a dipole force on the atoms that varied periodically in space - an optical lattice. When we now switched off the laser trap that confined the cloud in the direction of the lattice, the atoms were free to tunnel into empty lattice sites to the left and to the right, causing the cloud to expanded. For the laser powers used in our experiments (which determine the depth of the lattice wells and hence the tunneling probability) the cloud expanded to about four times its initial size in 200 milliseconds (see Figure 3). We then repeated the experiment with the same laser powers, but this time we shook the reflecting mirror (which was mounted on a piezo-electric transducer) back and forth. As a result, the cloud of atoms now expanded less in the same time (8). Indeed, if the amplitude and frequency of the shaking were chosen appropriately, the expansion could be stopped completely!

Although this may come as a surprise - one might expect a strongly shaken quantum system to expand more rather than less - it is easy to write down the mathematical equations that explain this behaviour. In fact, the external driving can be absorbed into the theoretical description by using so-called Floquet states, which are ubiquitous in studies of classical and quantum systems with an explicit periodic time dependence (2,5). For the case of particles tunneling between lattice sites this leads to an effective tunneling parameter Jeff given by



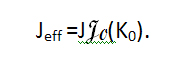
In this formula J is the "bare" tunneling parameter of the stationary lattice that characterizes how easily an atom can tunnel between sites. The bare J is multiplied by a zero-order Bessel function J0 which has as its argument the shaking parameter K0 (given by the ratio of the strength and frequency of the shaking). Since the Bessel function goes to zero for K0 = 2.4, 5.2...., this formula predicts that at these values of the shaking the parameter, Jeff also goes to zero and tunneling is suppressed - which is exactly what we found in our experiments.



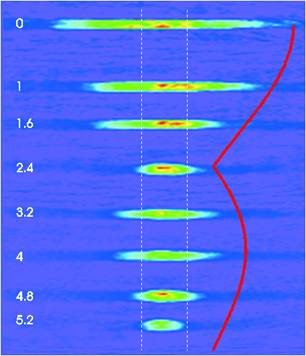
FIGURE 3: Dynamical localization of Bose condensates tunneling inside a shaken optical lattice (in-situ absorption pictures). For particular values of the shaking strength K0 (indicated on the left) tunneling is suppressed completely. The vertical white dashed lines indicate the width of the condensate at t=0, and the red line is the theoretical prediction (modulus of the zero-order Bessel function of K0).


Swinging “upside down”: the negative tunneling parameter

Another expected consequence of the above equation is the appearance of a negative effective tunneling parameter in the regions where the Bessel function becomes negative, e.g. between the first two zeroes at K0=2.4 and K0=5.2. As can be seen in Figure 3, in the expansion experiment the sign of Jeff does not seem to matter. That the extra minus sign in the effective tunneling parameter is actually there can, however, be demonstrated using a simple trick. This involves creating a matter-wave interference pattern very similar to an optical interference pattern in a multiple slit experiment. Rather than shining coherent light on an array of thin openings in a screen, one releases the atoms trapped in the optical lattice and allows their wavefunctions to spread out and overlap each other. After a short time (about 20 milliseconds in practice) one takes a snapshot of the atomic distribution which exhibits a pattern of bright and dark stripes, just as in the optical analogue (incidentally, a nice demonstration of the wave nature of atoms). If the atoms in all the lattice sites have the same phase, this interference pattern will have a dominant bright peak in the middle and smaller peaks at regular distances on either side of it (Figure 4(a)). In the case of a negative Jeff, however, the extra minus sign means that atoms in neighbouring lattice sites must have opposite phases (this is called a staggered state) as shown in Figure 4(b). The result is that the interference pattern is shifted and now exhibits two equally bright peaks centred about the forward direction indicated by the arrow in Figure 4. This shifting of the interference pattern is a clear indication that we have, indeed, created the quantum equivalent of the inverted pendulum shown in Figure 1.


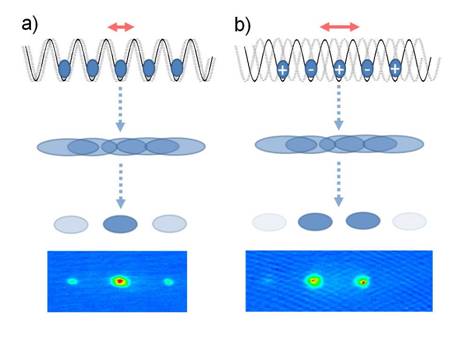
FIGURE 4: Atoms released from shaken optical lattices with a positive (a) and a negative tunneling parameter (b) produce distinctive interference patterns that contain information about the relative phases of atoms in adjacent wells. For the negative tunneling parameter in (b), a staggered state is created in which neighbouring wells have opposite phases. The pictures at the bottom were obtained experimentally by imaging the interfering atoms around 20 milliseconds after they had been released from the optical lattice.

Taking all of the above together we conclude that by periodically shaking our optical lattices we can essentially tell the atoms what to do: move slowly, stop completely or “swing upside-down”. A simple vibrating mirror in our setup, therefore, allows us to tune the tunneling dynamics of the atoms to our needs. This is an extension to matter waves of a concept that is well-known in atomic physics: the dressed atom (9). In the dressed atom picture, the behaviour of an atom in a strong laser field is explained by “dressing” its quantum states with those of the laser photons. Similarly, we can call the quantum states that we produce by shaking optical lattices “dressed matter waves” (10).


Shaking atoms to order

In order to demonstrate the usefulness of that picture, we performed an experiment in which we dressed the rubidium atoms in such a way as to make them undergo a quantum phase transition from a superfluid to a Mott insulating state and back. That phase transition was theoretically studied for bosons in crystal lattices in the 1980s (11) and experimentally realized with cold atoms in lattice in 2002 (12). The idea behind it is that when particles in a crystal lattice are prevented from tunneling freely between the lattice sites, Heisenberg's uncertainty principle tells us that the increased knowledge of the position of an individual particle has to be compensated by a decrease in the knowledge of its quantum-mechanical phase. Ultimately, in the Mott insulating state all the particles are pinned down to a well-defined lattice site, and their relative phases must therefore be completely random. This also means that we can detect this phase transition by observing the interference pattern of the atoms: once the phases are randomized, the interference peaks in Figure 4 become blurred and indistinguishable. It is straightforward to extend our methods described above to three-dimensions, and our setup for realizing the Mott insulating transition is shown in Figure 5. In order to induce the quantum phase transition all we had to do was to load our Bose condensates into shallow optical lattices in which the atoms could tunnel easily between sites. After that, we started shaking all three lattices more and more until the effective tunneling parameter was reduced sufficiently in order for the phase transition to occur. At that point, the peaks of the interference pattern became blurred as expected, but appeared again when we stopped shaking the lattices so that tunneling could resume (13).


Perspectives
Being able to tell quantum particles what to do simply by appropriately shaking them around suggests new applications in the quantum control of cold atoms. In fact, the “dressed matter waves” thus created can exhibit properties that are hard to find in naturally occurring systems, such as the negative tunneling parameter mentioned above. In a triangular lattice, such a negative Jeff can, for instance, mimic frustrated spin systems (14) and also simulate other complicated Hamiltonians that are difficult to study in solid state materials. Also, the properties of the Floquet states that govern the dynamics of particles in strongly driven potentials are not fully understood yet. In particular, it is still an open question how Floquet states can adiabatically follow a parameter variation in the driving. These and other problems can now be experimentally studied with cold atoms in optical lattices.




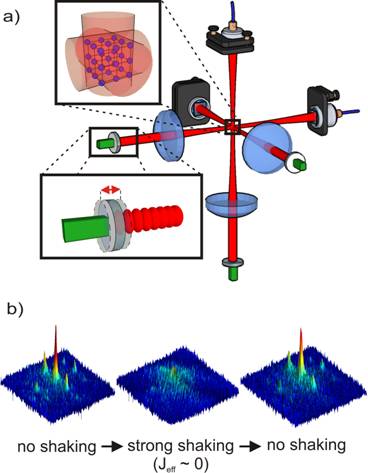
FIGURE 5: Experimental setup for a three-dimensional shaken optical lattice (a). The bottom blow-up shows a retro-reflecting mirror mounted on a vibrating piezo-electric transducer that causes the standing wave to shake back and forth. In this setup the superfluid to Mott insulator transition can be induced by loading the atoms into a static lattice in which they can tunnel freely and then increasing the amplitude of the shaking until the effective tunneling parameter is sufficiently small. The phase transition shows up in an interference pattern as a vanishing of the clear interference peaks (b). By decreasing the shaking amplitude this transition can be reversed.

Acknowledgements:

The authors would like to thank the PhD students and post-docs participating in the experiments described in this article: H. Lignier, C. Sias, A. Zenesini, Y. Singh and J. Radogostowicz. We acknowledge funding by the MIUR (PRIN-2007), OLAQUI (EC FP6-511057), and NAMEQUAM (EC FP7-225187).

About the authors:

Oliver Morsch studied physics at Oxford University, where he received his B.A. in 1995 and completed his D.Phil. thesis in 1999. He then moved to Pisa, Italy, first as a Marie Curie Fellow and subsequently as Senior Researcher at the CNR (National Research Council). His research interests include Bose Einstein condensates, optical lattices and Rydberg atoms.

Donatella Ciampini is a researcher at the Faculty of Science of the University of Pisa, from which she received her Ph.D.in 2002. Her main research interests are in the field of light-matter interaction in Bose-Einstein condensates: ultra-cold collisions, photoionization and Rydberg atoms excitation, quantum transport in optical lattices, dynamical localization in periodically driven systems and dressed matter-waves.

Ennio Arimondo studied physics at the University of Pisa and the Scuola Normale Superiore in Pisa. Since 1980 full professor, first appointment at the University of Naples and later at the University of Pisa.

More information about the research group can be found at: www.df.unipi.it/gruppi/struttura/index.htm.

References:

(1) E.I. Butikov, Am. J. Phys 69, 755 (2001).
(2) F. Grossmann, T. Dittrich, P. Jung, and P. Hänggi, Phys. Rev. Lett. 67, 516 (1991).
(3) E. Kierig, U. Schnorrberger, A. Schietinger, J. Tomkovic, and M.K. Oberthaler, Phys. Rev. Lett. 100, 190405 (2008).
(4) R.E. Merrifield, J. Chem. Phys. 28, 647 (1958).
(5) D.H. Dunlap and V.M. Kenkre, Phys. Rev. B 34, 3625 (1986).
(6) O. Morsch and M. Oberthaler, Rev. Mod. Phys. 78, 179 (2006).
(7) I. Bloch, J. Dalibard, and W. Zwerger, Rev. Mod. Phys. 80, 885 (2008).
(8) H. Lignier, C. Sias, D. Ciampini, Y. Singh, A. Zenesini, O. Morsch, and E. Arimondo, Phys. Rev. Lett. 99, 220403 (2007).
(9) C. Cohen-Tannoudji, Cargèse Lectures in Physics, (ed. M. Lévy) Vol. 2, 347 (Gordon and Breach, 1968).
(10) A. Eckardt, C. Weiss, and M. Holthaus, Phys. Rev. Lett. 95, 260404 (2005).
(11) M.P.A. Fisher, P.B. Weichman, G. Grinstein, and D.S. Fisher, Phys. Rev. B 40, 546 (1989).
(12) M. Greiner, O. Mandel, T. Esslinger, T.W. Hänsch, and I. Bloch, Nature 415, 39 (2002).
(13) A. Zenesini, H. Lignier, D. Ciampini, O. Morsch, and E. Arimondo, Phys. Rev. Lett. 102, 100403 (2009).
(14) A. Eckardt, P. Hauke, P. Soltan-Panahi, C. Becker, K. Sengstock, and M. Lewenstein, Europhys. Letters 89, 10010 (2010).